Bevezetés

Gyakran magyarázó és elõrejelzõ erõvel rendelkezik az emberi viselkedés tanulmányozásakor az a feltevés, hogy az adott személy racionálisan viselkedett vagy viselkedik. E feltevés segítségével néhány meglehetõsen egyszerû hipotézissel élve magyarázni vagy jósolni tudunk nagyszámú igen bonyolult tényt egy adott személy céljaival és viselkedésével kapcsolatban.

Tegyük fel például, hogy egy történész arra a meggyõzõdésre jut, hogy Napóleon meglehetõsen racionálisan cselekedett néhány idõszakon át. Azaz Napóleon cselekedetei ebben az idõszakban megmagyarázhatóak politikai és katonai körülményei segítségével - lehetõség szerint viszonylag kevés tény felhasználásával -, másképpen fogalmazva, pszichológiai változók nem kellenek magatartása kifejtéséhez. Viszont ha történészünk úgy találja, hogy Napóleon magatartása nem volt túlságosan racionális, ebbõl az következhet, hogy a meglehetõsen jól definiált politikai tényeknek nincs olyan halmaza, amelynek segítségével magyarázni tudnánk Napóleon magatartását. Bármely elfogadható magyarázathoz szükséges élni "mélyebb" motivációs tényezõkkel és néhány specifikus feltevéssel az adott személy lélektani mechanizmusairól.

Természetesen az a kérdés, hogy ténylegesen mennyire racionális Napóleon magatartása, nemcsak azért fontos, hogy megmagyarázzuk a viselkedését, de az esemény leírásához is. Például bármely leírás Napóleon politikai és katonai döntéseirõl nagyon hiányos lenne, még leíró szinten is, ha nem tárgyalná ezeknek a döntéseknek a racionális vagy irracionális voltát. Így nem lenne elegendõ kifejteni azt, hogy egy adott csatában Napóleon megtámadta az ellenség jobb szárnyát. Bármely az adott viselkedést kielégítõen magyarázó elemzésnek meg kell azt a kérdést is válaszolnia, hogy ez megfelelõ - vagy adott esetben kiváló - taktikai húzás volt-e, avagy sem.
 

A racionális magatartás mint hasznosság-maximalizálás

A közgazdaságtan azt állítja, hogy a racionális magatartás a konzisztens preferenciákon alapszik. Ha egy adott személy preferenciái kielégítenek néhány alapvetõ konzisztencia-kritériumot, akkor ezeket a preferenciákat egy jól definiált hasznosságfüggvény matematikai apparátusának feleltethetjük meg. Így a racionális magatartás a hasznosságfüggvény maximalizálásának, azaz hasznosság-maximalizálásnak tekinthetõ. Ebbõl az következik, hogy a racionális magatartásnak ezt a definícióját a hasznosságelméletnek (utility theory) nevezem.

Rengeteg bizonyíték van arra, hogy ez a feltevés nem teljesül, mégis a közgazdaságtan azon a feltevésen nyugszik, hogy az emberek preferenciái teljesen konzisztensek. A legtöbb közgazdász úgy tekint erre, mint hasznos leegyszerûsítõ feltevésre, úgy érvelve, hogy az a közgazdaságtudomány, melyet erre a feltevésre építünk, általában meglehetõsen jó, ha nem is teljesen megfelelõ elõrejelzéseket ad a gazdasági rendszer mûködésérõl.

Számos közgazdász azt az álláspontot foglalja el, hogy a közgazdaságtan hasznos szerepet játszhat a társadalmi magatartás változásainak magyarázatában a gazdasági életen kívül is. Az elmúlt száz évben például az átlagos családméret a legtöbb országban jelentõsen csökkent. Érvelhetünk azzal, hogy a nagy család gazdasági elõnyei lényegesen lecsökkentek, ezzel szemben a költségei nagymértékben megnövekedtek az urbanizáció és az iparosodás miatt. A kisebb családok iránti pozitív társadalmi beállítódás szintén fontos szerepet játszott.

A társadalmi beállítódások ezen változásai másfelõl maguk is a gazdasági változások eredményei lehetnek. Gyakran igaz a társadalomtudományokban, hogy hasonló kérdésekre nem tudunk egyszerû választ adni.
 

Döntéselmélet

Eredeti formájában a hasznosságelmélet racionális magatartáskoncepciója a "bizonyosság" esetére vonatkozott csak. Azaz olyan esetekre, amikor a döntéshozó biztos vagy majdnem biztos volt, hogy cselekedetének milyen következményei lesznek vagy lehetnek.

A döntéselmélet feladata ennek a racionalitásfelfogásnak a kiterjesztése a bizonytalanság esetére, azaz azokra az esetekre, amikor a döntéshozó bizonytalan cselekedetének következményeit illetõen.

A modern döntéselmélet a bayesi megközelítésen nyugszik (Thomas Bayes 18. századi angol matematikus volt). Bayes azzal a feltevéssel élt, hogy ha nem tudjuk, mit hoz a jövõ, akkor rendeljünk valószínûségeket a lehetséges eseményekhez és használjuk ezeket a valószínûségeket annak eldöntéséhez, hogy mit is tegyünk.

A bayesi megközelítésnek megfelelõen a modern döntéselmélet a következõt javasolja a döntéshozónak arra az esetre, ha bizonytalan döntése következményeit illetõen. Elõször is valószínûségeket kell rendelnie minden lehetséges következményhez a rendelkezésre álló legjobb információk alapján. Ezután ki kell számolnia mindegyik cselekedete várható hasznosságát a lehetséges következmények valószínûségei és hasznosságai alapján. A valószínûségszámítás meglehetõsen egyszerû képletet ad a várható hasznosság kiszámításához.

Ha a várható hasznosságok ismeretesek, akkor a döntéshozó racionális magatartásának az felel meg, ha azt a döntést választja, amelyik a legnagyobb várható hasznosságot eredményezi.

Szeretném ehhez hozzáfûzni, hogy a racionális magatartásnak ez a definíciója csak azoknál a döntéseknél használható, amikor a döntéshozó preferenciái kielégítenek néhány erõsebb konzisztencia-követelményt, mint amilyeneket a hasznosságelmélet esetében feltettünk.
 

A racionális magatartás általános elmélete

A modern döntéselmélet racionalitásfelfogása további általánosításokat igényel, mivel az eddigiek nem elégségesek a játékhelyzetek magyarázatához. Azaz azoknak a helyzeteknek a magyarázatához, ahol a végeredmény két vagy több teljesen vagy részlegesen eltérõ érdekû szereplõ cselekedeteitõl függ. A játékhelyzetek maguk úgy tekinthetõk, mint amelyek bizonytalanságot tartalmaznak, mivel egyik játékos sem jelezheti elõre a tényleges kimenetelt vagy akár a lehetséges kimenetelek valószínûségét.

Pontosabban fogalmazva, egyik játékos sem tud ilyen elõrejelzéseket tenni a helyzetek játékelméleti elemzése nélkül, és ilyen elemzéseket a klasszikus döntéselmélet nem tud adni.

A hasznosságelmélet, a döntéselmélet és a játékelmélet mellett az etika az, amelyet a racionális magatartás általános elmélete részének tartok, mint ahogy azt korábbi publikációimban a morális magatartás döntéselméleti megalapozásával bizonyítani próbáltam. (Pontosabban, amellett érveltem, hogy a morális magatartás definiálható mint a racionális egyének magatartása, akik tudatában vannak annak, hogy hasonló valószínûséggel kerülhetnek bármely pozícióba az adott társadalomban. Ezért a morális magatartás definiálható mint a társadalom összes egyéneinek az általános hasznossági szint maximalizálására irányuló cselekvése.)

A racionális magatartás általános elméletének különbözõ ágait mutatja be a következõ ábra:
 

A legjobb válaszok és a Nash-egyensúly

Az alábbiakban a játékelmélet néhány alapgondolatát tárgyalom. Tegyük föl, hogy az adott i játékos valamely s_i stratégiát alkalmaz a játék során. Tegyük fel továbbá azt is, hogy ismerve a többi játékos stratégiáit, ez az s_i az összes stratégia közül a legmagasabb hozamot eredményezi. Ekkor s_i-t a legjobb válasznak nevezzük az adott játékos stratégiái közül. Nash-egyensúlyról akkor beszélünk, amikor az összes játékos stratégiája a legjobb válasz a többi játékos stratégiáira.

A Nash-egyensúly gondolata John Nash-tõl származik, akit szintén 1994-ben tüntettek ki Nobel-díjjal. Nash megmutatta azt is, hogy minden véges játéknak van legalább egy egyensúlyi pontja. (Számos esetben több egyensúlyi pont létezik.)
 

Kooperatív és nem kooperatív játékok

Nash felosztotta a játékokat kooperatív és nem kooperatív játékokra. A kooperatív játék olyan játék, melyben a játékosok közötti együttmûködés kikényszerítõdik. Nem kooperatív játékokról akkor beszélünk, amikor a játékosok között nem lehet egyességet kikényszeríteni.

Egy nem-kooperatív játék a játékosok adott stratégiái esetén akkor és csak akkor stabil, ha létezik Nash-egyensúly. Stabil, ha létezik Nash-egyensúly, mivel ebben az esetben az egyes játékosok stratégiái a legjobb válaszok más játékosok stratégiáira, így egyik játékos sem akar ebbõl az állapotból kimozdulni, más stratégiát választva. Másfelõl a játék nem lesz stabil, ha nincs Nash-egyensúlyi pont, hiszen ebben az esetben mindig lesz legalább egy játékos, akinek a stratégiája nem a legjobb válasz, és ezért érdekelt lesz abban, hogy új stratégiát válasszon.

A kooperatív játékok esetén még akkor is stabil lehet, ha egy stratégia-kombináció nem Nash-egyensúly, amennyiben a játékosok egyezségre jutnak, hogy ezt a stratégia-kombinációt válasszák.
 

Egy példa a fenti elméletre

Tekintsük a következõ G játékot:

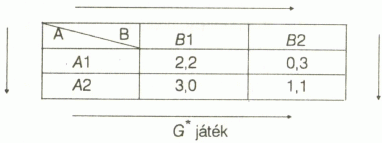
Ebben a játékban az A játékosnak két stratégiája van, A1 és A2, míg a B játékosnak szintén két stratégiája van, B1 és B2. A táblázat négy mezõjében az elsõ szám az A játékos nyereményét, míg a második szám a B játékos nyereményét jelenti. Ha a B játékos B1 stratégiát használja, akkor az A játékos legjobb válasza erre A2 stratégia, mivel három nagyobb, mint kettõ, azaz így maximalizálja a nyereményét. A fenti tényt lefelé mutató nyíllal jelzem. Ha a B játékos B2 stratégiát választja, akkor az A játékos legjobb válasza ismét A2, mivel egy nagyobb nullánál. Ezt a tényt a táblázat jobb oldalán lefelé mutató nyíllal jelzem. Másfelõl, ha az A játékos A1 stratégiát választja, akkor a B játékos legjobb válasza B2 stratégia, mivel három nagyobb, mint kettõ. Hasonlóan, ha az A játékos A2 stratégiát választja, akkor B játékos legjobb válasza B2, mivel egy nagyobb, mint nulla. Ezt a két tényt a két megfelelõ nyíl jelzi.

Világos, hogy az egyetlen Nash-egyensúlyi pont az (A2 B2) stratégiapár, mivel egyedül ez a kölcsönösen legjobb választ tartalmazó pont. Geometriailag ez azt a tényt jelenti, hogy a táblázat jobb alsó négyzete az egyedüli, ahova mind a függõleges, mind a vízszintes nyilak mutatnak.

Így, ha ezt a játékot mint nem kooperatív játékot játsszák, akkor a Nash-egyensúly (A2 B2) stratégiapár lesz, szokás ezt a nem kooperatív megoldásnak is nevezni.

Ha a játékot mint kooperatív játékot játsszák, akkor az (A1 B1) stratégiapár lesz a megoldás, s ezt kooperatív megoldásnak nevezik. A játék teljesen szimmetrikus a két játékosra nézve, ezért valószínûtlen az, hogy bármelyik játékos egyetértene olyan megoldásban, amely számára alacsonyabb nyereséggel járna, mint a másik játékos számára. Ez kizárja az (A1 82) és (A2 B1) stratégiapárokat mint lehetséges megoldásokat. Így marad az (A1 81) és az (A2 B2) stratégiapár. Mivel az utóbbi kisebb nyereséget eredményez mindkét játékos számára, ezért a valószínû végeredmény az (A1 B1) stratégiapár.

Megjegyezzük, hogy az elõbb elemzett játék kifizetési struktúrája többé-kevésbé hasonlatos a fogoly-dilemma néven közismert játékhoz. A fogoly-dilemma játékkal szokás illusztrálni a kooperatív és a nem kooperatív megoldások közötti különbséget.
 

Nem teljes információs játékok

Teljes információs játékról akkor beszélünk, ha az összes játékos teljes információval rendelkezik a játékot meghatározó összes paraméterrõl, így a különbözõ játékosok kifizetõ függvényeirõl, lehetséges stratégiáiról és a többi játékos fenti tényeket érintõ informáltságáról. Nem teljes információs játékról beszélünk az összes ettõl eltérõ esetben.

A klasszikus játékelmélet jelentõs korlátja volt az, hogy nem tudta kezelni a nem teljes információs játékokat. A gyakorlati életben elforduló legfontosabb játékok, játékelméleti helyzetek nem teljes információs játékok: a játékosok csak korlátozott ismeretekkel rendelkeznek a többiek kifizetõ függvényérõl (azaz a többiek valódi céljairól a játékban) és keveset tudnak a többi játékos stratégiáiról és a rendelkezésükre álló információról.

Az elmúlt néhány évben megoldás született arra, hogyan lehet ezt a nehézséget feloldani. Tekintsünk egy példát. Tegyük föl, hogy a fegyverkorlátozási tárgyalásokat akarjuk elemezni a hidegháború idején az Egyesült Államok és a Szovjetunió között.

Az alapvetõ nehézség az, hogy egyik tárgyaló fél sem ismerte a másik tényleges szándékait és technikai lehetõségeit. (viszonylag megbízható információkkal rendelkezhettek egymás aktuális fegyverkészletérõl, de nagyon keveset tudtak a katonai fejlesztésekrõl, amelyeket a másik fél a fegyvergyártásban alkalmazott.) A következõ modellt használhatjuk. Az amerikai játékos - jelöljük A-val - és az orosz játékos jelöljük R-rel - különbözõ lehetséges típusú lehet. Például az orosz játékos lehet R1 típusú, rendkívül békés szándékú és az új fegyvertechnológiákról kevés tudással rendelkezõ személy, azzal az elképzeléssel, hogy az amerikai játékos szintén békés szándékú, de új fegyverkezési technológiákat kíván alkalmazni. Lehet az orosz játékos R2 típusú is, aki ugyanolyan, mint az R1, azzal a különbséggel, hogy az amerikai játékosról rendkívül agresszív szándékokat tételez fel. Az orosz játékos esetleg lehet R3 típusú is, aki megint más tulajdonságkombinációkkal jellemezhetõ - és így tovább.

Hasonlóan, az amerikai játékos is lehet A1, A2, A3 stb. típusú, különbözõ tulajdonságok kombinációjával az új technológiák alkalmazását, az orosz szándékokat stb. illetõen.

A játékot a következõképpen játsszák. A játék kezdetén egy hipotetikus sorsolás dönt, hogy milyen amerikai és orosz játékostípus vesz részt a játékban. Mindegyik lehetséges (Ai Rj) játékospárhoz rendeljünk elõre egy p_ij valószínûséget. Amikor egy adott (Ai Rj) párt kiválasztunk, lejátsszák a játékot. Mindegyik játékos tudja a saját típusát, de nem vesz tudomást az ellenfele aktuális típusáról, ellenben az ellenfél összes lehetséges típusához hozzá tud rendelni egy valószínûséget annak megfelelõen, hogy milyen valószínûséggel lesz az ellenfél az adott típusú, hiszen ismeretes a p_ij valószínûség.

Ez a modell lehetõvé teszi, hogy az eredeti G játékot, amely nem teljes információs játék volt, felcseréljük egy új, G* játékra, amely már teljes információs játék lesz, és játékelméleti szempontból nézve megegyezik az eredeti G játékkal.

A G* játék teljes információs játék, mivel feltevéseink mellett mindkét játékos ismeri a p_ij valószínûségeket (még ha egymás aktuális típusát nem is), és ez lehetõvé teszi, hogy kiszámítsuk a játékosok saját és egymásra vonatkoztatott kifizetõ függvényeit az új játékban.

Másfelõl mivel a G* játék teljes információs, szemben az eredeti G játékkal, ez a tény lehetõvé teszi a játékelméleti elemzést. Gyakran számos, a valódi életben elõforduló játékelméleti helyzet nem teljes információs játék, és ez az új megközelítés lehetõvé teszi a valódi életben elõforduló játékok játékelméleti elemzését. Ez nagymértékben elõsegítette a játékelméleti modellek alkalmazását a matematikai közgazdaságtanban.