
ahol
Bevezetés
A kérdõíves kikérdezésen alapuló vizsgálatok egyik legnagyobb módszertani problémája, hogy bizonyos kérdésekre adott válaszok esetében nem bízhatunk meg az érvényességükben. A válaszadó valóságos és kinyilvánított véleménye közötti megfelelés hiányának több típusa ismeretes. Az egyik típusra az jellemzõ, hogy a válaszadónak nincs az adott kérdésben véleménye, de a helyzet vélt elvárásainak engedve mégis mond véleményt. A másik típusba tartozó esetekben a válaszadónak van véleménye, de hallgatással leplezi. A harmadik típus sajátossága az, hogy a válaszadónak van véleménye, de nem akarja, vagy nem meri kinyilvánítani, és helyette másik véleményt nyilvánít ki. Bármelyik típusról legyen szó, mindegyik esetben azt mondhatjuk, hogy a kérdés "érzékeny", azaz a válaszadók számára "kényes".
Az államszocialista rendszer idõszakában végzett közvélemény-kutatások során tapasztaltuk, hogy a válaszadók különösképpen a politikai témák esetében folyamodtak a véleményt elhallgató vagy a valódi véleményt leplezõ stratégiákhoz. Egy vizsgálat során azt találtuk, hogy amikor Magyarország és a Szovjetunió hasonlóságát kellett megítélni olyan dimenziókban (lelkialkat, történelmi sors, életszínvonal), amelyekben egyébként józan ésszel nehéz feltételezni a hasonlóságot, a válaszadók sokkal inkább említették a "nagy testvért", amikor az említhetõ alternatívák zárt sorában a Szovjetunió neve is szerepelt, mint a nyílt kérdezés esetén, amikor is azt az országot említhették, amelyik eszükbe jutott. Az eltérés magyarázata során arra a következtetésre jutottunk, hogy a kísérleti minta tagjait konform reakciókra késztette a Szovjetunió szerepeltetése a kérdõívben.
Demokratikus rendszerekben sem ismeretlen a válaszadói konformitás. A hamis válaszok motivációját ebben az esetben nem politikai, hanem erkölcsi dimenzióban célszerû keresni: a kérdezett azért érzi titkolandónak valódi válaszát, mert összeegyeztethetetlennek véli a nyilvánosságnak bemutatni kívánt önképével.
Olyan vizsgálatot terveztünk, amelynek az volt a célja,
hogy a poszt-szocialista nyilvánosság körülményei
között fényt derítsünk a megtévesztési
hajlandóságra.
1. A véletlenített kérdõíves technikával kapott adatok statisztikai elemzése
Az empirikus szociológiai felvételek adatait gyakran terhelik olyan hibák, amelyek torzítják a statisztikai elemzések eredményeit. Lehetnek mintahibák, mérési és véletlen hibák. A legtöbb gondot a mérési hibák okozzák, és közülük is azok, amelyek nem technikai, vagyis kérdezési, kódolási vagy rögzítési tévedések, hanem szubjektív tényezõkbõl fakadnak.
A társadalmi jelenségek mélyebb okainak vizsgálata során a kutató gyakran ütközik olyan tényekbe, viselkedési formákba, amelyek valamilyen oknál fogva nem legálisak, a közösség által nem elfogadottak, deviánsnak minõsülnek, vagy a magánélet olyan szférájába tartoznak, amirõl az emberek nem szívesen nyilatkoznak. Ezekrõl a jelenségekrõl kérdõíves technikával adatokat gyûjteni igen nehézkes, sok kérdezett megtagadja a választ, vagy ha válaszol is, nem okvetlenül õszinte választ ad, annak ellenére, hogy biztosítjuk az adatok névtelen feldolgozásáról. Így az eredmények erõsen torzítottak lesznek.
Ha például kényes kérdések esetében kategóriák között kell választania a kérdezettnek, sok esetben feltételezhetõ, hogy nem abba a kategóriába sorolja magát, ahová valójában tartozna, hanem egy másikba. Ilyen esetben az egyik lehetséges eljárás az, hogy az elemzések során figyelembe vesszük, hogy hibásan besorolt adatokkal kell számolnunk, és ennek megfelelõen módosítjuk a következtetéseinket (Bross 1954; Assakul-Proctor 1967; Cohran 1968; Tenenbein 1970; Korn 1981; Bornemisza 1994) - így eldönthetjük, hogy az elvégzett statisztikai elemzések milyen mértékben tekinthetõk érvényesnek a változók valós (meg nem figyelt) eloszlására. A vizsgálatok egy részénél szükség van a hibás besorolások valószínûségeinek ismeretére, erre azonban elég ritkán van mód.
A másik lehetséges eljárás olyan kérdezési technika alkalmazása, amely - a kérdezett számára is meggyõzõen - kizárja az azonosíthatóságot (Fox-Tracy 1987; Rudas 1979). Ez a kritérium különbözõ véletlenítési technikákkal teljesíthetõ. E módszereknek az a közös kiindulópontja, hogy a kérdezettnek az érzékeny kérdésen kívül semleges kérdés(ek) is rendelkezésére áll(nak), és, hogy ezek közül melyikre válaszol, olyan véletlen kísérlettel kell eldöntenie, amelynek kimenetelét a kérdezõ nem láthatja. Ha a kutató ismeri a véletlen kísérlet kimeneteleinek valószínûségi megoszlását, akkor (feltéve, hogy a kérdezettek védettségük tudatában õszintén válaszoltak) torzítatlan becslést adhat az érzékeny kérdésre kapott válaszok mintabeli megoszlására. Az eljárás hátránya egyrészt az, hogy a becslés szórása lényegesen megnövekszik, másrészt az, hogy az érzékeny kérdésekre adott válaszokat nem ismerjük pontosan, értéküket csak bizonyos valószínûséggel tudjuk, így a szokásos többváltozós elemzések nem, vagy csak nagyon korlátozott mértékben alkalmazhatók a véletlenített kérdezési technikával kapott adatokra.
Ennek a tanulmánynak a célja, hogy megmutassa diszkrét
változók esetén egy egyszerû véletlenítési
eljárás mellett az érzékeny kérdésre
kapott válaszok megoszlására vonatkozó némely
becslés tulajdonságait, két változó
kapcsolatára vonatkozó hipotézisek próbáinak
alkalmazási feltételeit és azokat a módosításokat,
amelyek révén több változóra vonatkozó
log-lineáris modelleket lehet elemezni. Ezeket a vizsgálatokat
a hibásan besorolt adatok elemzésére kidolgozott módszerek
eredményeinek felhasználásával végezzük
el.
2. A véletlenítési eljárás
A véletlenítési eljárásoknak több változata szolgál olyan egymásnak ellentmondó kívánalmak optimalizálására, mint az, hogy egyfelõl a kérdezett eléggé rejtve érezze magát a válaszadáskor, másfelõl a vizsgált jelenség elõfordulási valószínûségére adott becslés szórása minél kisebb legyen. A véletlenítési módszerek legelsõ, Warner (1965) által kidolgozott eljárásában a kérdezett két kérdést kapott, amelyek közül az egyik volt az érzékeny kérdés, a másik ennek a logikai ellentéte. Azt, hogy melyik kérdésre válaszol, véletlen kísérlet dönti el, amelynek a kimenetelét csak õ ismeri. A kérdezõ ezután lejegyzi az õ igen vagy nem válaszát, anélkül, hogy tudná, hogy a válasz melyik kérdésre vonatkozik. A két kérdés lehet például az, hogy
1. Igaz-e, hogy Ön csalt már az adó bevallásakor?
2. Igaz-e, hogy Ön sosem csalt még az adó bevallásakor?
A véletlen kísérlet lehet kockadobás: megadhatjuk, hogy mely számok dobásakor válaszoljon a kérdezett az elsõ kérdésre, és melyeknél a másodikra, vagy lehet kártyahúzás megkevert kártyacsomagból, amelyben a lapok meghatározott részén az 1., más részükön a 2. kérdés szerepel.
Az alternatív kérdések ilyetén megfogalmazásakor a kérdezett gyanakodhat arra, hogy mivel mindkét kérdés ugyanarra a dologra vonatkozik, valamilyen matematikai trükkel mégis vissza lehet következtetni arra, hogy õ rendelkezik-e az elítélhetõ jellemzõvel. Ezt a problémát kerüli el az a Simmons által javasolt megoldás, melyben csak az egyik kérdés vonatkozik az érzékeny jellemzõre, a másik egy tetszõleges, de legkevésbé sem elítélhetõ jellemzõre vonatkozik, például
1. Csalt-e már Ön az adó bevallásakor?
2. Elõfizet-e Ön valamilyen újságra?
A véletlenítési eljárás ugyanolyan lehet, mint az elõzõ esetben, és bár valószínûleg az így megfogalmazott kérdéspárnál nagyobb együttmûködési készséget és õszintébb válaszadást várhatunk, az elemzéseket nehezíti, hogy a 2. kérdésre adott válaszok pontos eloszlását nem ismerjük. Segíthetünk ezen, ha olyan kérdést teszünk fel, amelynek ismert a megoszlása, például, hogy az év bizonyos hónapjában született-e a kérdezett (Bradburn-Sudman 1979), bár itt is adódhatnak a területi statisztikák különbözõségébõl fakadó nehézségek. A másik lehetséges megoldás Moors (1971) javaslata alapján az, hogy a minta egy részét csak arra vesszük igénybe, hogy a 2. kérdésre adott válaszok megoszlását becsüljük, és a másik részén végezzük a véletlenített kérdezést az 1. és 2. kérdéssel. Folsom és munkatársai (1974) továbbfejlesztették ezt a módszert abból kiindulva, hogy sokkal jobb eredményt várhatunk akkor, ha a két almintának a 2. kérdésként két semleges alternatív kérdést teszünk fel, és ezeket a két almintán felváltva használjuk véletlenítésre és direkt kérdezésre, például
az elsõ almintán
véletlenített eljárás:
1. Csalt-e már Ön az adó bevallásakor?
2. Hallgatta Ön a 10 órás híreket
tegnap este?
direkt kérdés:
3. Elõfizet Ön valamilyen újságra?
a második almintán
véletlenített eljárás:
1. Csalt-e már Ön az adó bevallásakor?
2. Elõfizet Ön valamilyen újságra?
direkt kérdés:
3. Hallgatta Ön a 10 órás híreket tegnap
este?
Ezzel az eljárással az egyes almintákon a másik alminta alternatív kérdésre adott válaszok megoszlását megbecsülhetjük, de természetesen maga ez a becslés is tovább növeli az érzékeny jellemzõ megoszlására vonatkozó becslések szórását.
Mindezeket a buktatókat elkerüli a Stem és Steinhorst (1984) által javasolt "erõltetett alternatíva" módszer, amely szerint alternatív kérdés helyett különbözõ utasításokat kap a kérdezett, és a véletlen kísérlet kimenetele alapján választ közülük. Az utasítások:
1. Kérem, válaszolja azt, hogy "nem".
2. Kérem, válaszoljon a kérdésre: "Csalt-e
már Ön az adó bevallásakor?".
3. Kérem, válaszolja azt, hogy "igen".
A tapasztalat azt mutatja, hogy bár ez az eljárás eléggé "steril", és a kérdezett elvileg könnyen beláthatja, hogy elítélhetõ jellemzõje rejtve marad, azok, akik ezzel nem rendelkeznek, nem szívesen válaszolják azt, hogy "igen", ha ezt az utasítást kapják.
A fenti eljárások bármelyikét választva, a véletlen kísérlet megtervezésekor a leglényegesebb kérdés annak a meghatározása, hogy a kísérlet kimeneteleinek milyen legyen a megoszlása. Minél közelebb van ez az egyenletes eloszláshoz, annál inkább rejtve érezheti magát a kérdezett, mert körülbelül egyformán sok alternatívát lát, ekkor viszont az elítélhetõ jellemzõ megoszlására vonatkozó becslés lesz nagyon bizonytalan, vagyis nagy szórású. Viszont ha nagyon túlsúlyban vannak az elítélhetõ jellemzõ meglétére vonatkozó kérdések, a becslések pontosabbak lesznek, de a kérdezettek vonakodnak majd attól, hogy õszinte választ adjanak.
A továbbiakban az elsõ, Warner-féle eljárással
kapott adatok statisztikai elemzésének módszereit
mutatjuk be.
3. Hibásan besorolt adatok és véletlenített kérdõíves technikával kapott adatok összehasonlítása
A bevezetõben már említettük, hogy érzékeny kérdések esetén a direkt kérdezési technikával kapott adatokat gyakran terhelik mérési hibák. Ilyen például az, hogy diszkrét változóknál az esetek egy részét nem abba a kategóriába soroljuk be a kapott válaszok alapján, ahova valójában tartozna, hanem egy másikba. A meg nem figyelt valós, és a hibával megfigyelt binomiális eloszlású változók elõfordulási gyakoriságaira vonatkozó összefüggéseket az 1. táblázatban foglalhatjuk össze:
1. táblázat

ahol
p a populációban az elsõ kategória valós elõfordulási valószínûsége,
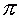 az elsõ kategória elõfordulási
valószínûsége hibás besorolással
történõ megfigyelésnél,
az elsõ kategória elõfordulási
valószínûsége hibás besorolással
történõ megfigyelésnél,
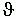 1 az elsõ kategóriába
tartozók hibás besorolásának valószínûsége,
1 az elsõ kategóriába
tartozók hibás besorolásának valószínûsége,
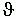 2 a második kategóriába
tartozók hibás besorolásának valószínûsége.
2 a második kategóriába
tartozók hibás besorolásának valószínûsége.
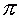 értékét a hibával megfigyelt
mintából A elsõ kategóriájában
az elõfordulások relatív gyakoriságával
becsüljük:
értékét a hibával megfigyelt
mintából A elsõ kategóriájában
az elõfordulások relatív gyakoriságával
becsüljük:
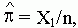 (3.1)
(3.1)
ahol X1 az A=1 megfigyelt értéke.
A hibás besorolások következtében az elsõ kategóriába esõ megfigyelések várható gyakorisága:
E(X1) = np+n(1-p)np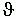 2-np
2-np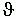 1
(3.2)
1
(3.2)
és várható relatív gyakorisága:
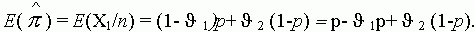 (3.3)
(3.3)
A Warner eljárása szerint véletlenített kérdõíves technikával kapott gyakoriságok pedig a következõ táblázatban foglalhatók össze:
2. táblázat

ahol
p a populációban az elsõ kategória valós elõfordulási valószínûsége,
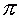 az elsõ kategória elõfordulási
valószínûsége véletlenített kérdõíves
technikával történõ megfigyelésnél,
az elsõ kategória elõfordulási
valószínûsége véletlenített kérdõíves
technikával történõ megfigyelésnél,
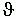 a negatív kérdések elõfordulási
valószínûsége a kérdõívben.
a negatív kérdések elõfordulási
valószínûsége a kérdõívben.
Az 1. és 2. táblázatok összehasonlításából látható, hogy a véletlenített kérdõíves technikával kapott gyakoriság-megoszlás megfeleltethetõ azonos hibás besorolási valószínûségek mellett a hibával mért adatok megoszlásával, így az utóbbiakra vonatkozó eredményeket alkalmazhatjuk a véletlenített kérdõíves adatokra.
A 2. táblázat alapján a valós megoszlás p paraméterére a következõ összefüggés alapján adható becslés:
 ahonnan
(3.4)
ahonnan
(3.4)
 (3.5)
(3.5)
amely torzítatlan becslés p-re.
A p-re vonatkozó becslés szórása pedig a binomiális eloszlás alapján:
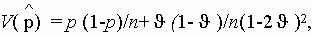 (3.6)
(3.6)
amely képletbõl látható, hogy a p-re ilyen
módon adott becslés szórása a direkt és
pontos megfigyeléssel kapható szóráshoz képest 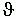 (1-
(1-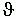 )/n(1-2
)/n(1-2 )2
taggal növekszik, amely akkor lenne minimális, ha
)2
taggal növekszik, amely akkor lenne minimális, ha 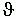 0 vagy 1 értéket venne fel, azaz csak az egyik vagy másik
kérdést tennénk föl, véletlenítés
nélkül.
0 vagy 1 értéket venne fel, azaz csak az egyik vagy másik
kérdést tennénk föl, véletlenítés
nélkül.
Ha tehát csak egy, véletlenített kérdõíves
eljárással vizsgált változót tekintünk,
annak az elõfordulási valószínûségeire
torzítatlan, de a valóságosnál nagyobb szórású
becslést adhatunk. Több változó együttes
vizsgálatánál azonban nem ilyen egyszerû a helyzet,
mert az egyes megfigyelések valós értékeire
nem tudunk becslést adni, ekkor azonban alkalmazhatjuk a hibás
besorolással kapott adatokra kidolgozott eredményeket (Bornemisza
1994).
4. A 2x2-es kontingencia-tábla vizsgálata
Elõször vizsgáljuk meg azokat az eseteket, amikor a két változó közül csak az egyik véletlenített, és a másikat csoportosító változónak tekintjük. Ebben az esetben homogenitás-vizsgálatot végezhetünk egy tulajdonság vagy jelenség csoportok közötti összehasonlításra. Ha a két megfigyelt csoport jellemzõjét ugyanazzal a véletlenítési eljárással vizsgáljuk, akkor ez a szituáció megegyezik azzal, amikor a csoportokon azonos hibás besorolási valószínûségek mellett figyeljük meg ezt a jellemzõt. Így a véletlenített kérdõíves technikával kapott adatokra is érvényes az az állítás, hogy a csoportok közötti különbséget a véletlenítési eljárás csökkenti. Mivel azonban a homogenitás hipotézise alatt a csoportok közötti különbségek a valós és véletlenítéssel kapott megoszlások mellett egymás többszörösei, így a különbségekre vonatkozó teszt érvényessége nem változik, vagyis a homogenitás-vizsgálat elsõfajú hibája a megfigyelt és a valós megoszlásnál megegyezik. A becslések szórásának növekedése miatt azonban a nem-centrális ?2 eloszlás nem-centralitási paramétere nagyobb lesz mint a valós eloszlás mellett, így a homogenitás-vizsgálat másodfajú hibája megnõ, vagyis a próba ereje csökken. Ez a két állítás igaz akkor is, ha a kontingencia-táblának csak a mintaelemszáma rögzített, vagyis a csoportok elemszáma véletlen változó, és akkor is, ha a minta rétegzett, vagyis a kontingencia-tábla egyik marginálisa rögzített.
Ha a csoportok közötti relatív esélyt vizsgáljuk, azaz a
 (4.1)
(4.1)
mennyiséget, ahol p1, illetve p2 a két csoportban a jelenség valós elõfordulási valószínûsége, akkor a csoportok között megegyezõ félreosztályozásokkal analóg módon azt állapíthatjuk meg, hogy a véletlenített eljárással történõ megfigyelés a valós relatív esélyt, vagyis a csoportosító és válaszváltozó közötti asszociációt csökkenti.
Tekintsük most azt az esetet, amikor a 2x2-es vagy ennél
nagyobb, rxc méretû kontingencia-táblában
mindkét változót véletlenítési
eljárással vizsgáltuk. Kézenfekvõ feltételezés,
hogy a két változóra kérdezve a véletlenítési
kísérleteket egymástól függetlenül
végezzük, vagyis az egyik kísérlet kimenetele
nem befolyásolja a másikat. A kísérletek kimeneteleinek
eloszlása a két változó mérésekor
azonban lehet különbözõ. A két változó
függetlenségét vizsgálva alkalmazhatjuk a független
félreosztályozásokkal megfigyelt változók
függetlenségi vizsgálatára vonatkozó állításokat,
és megállapíthatjuk, hogy a függetlenség
hipotézise a valós és a véletlenített
eljárással kapott megoszlásra ekvivalens, így
a megfigyelt adatokra vonatkozó próba szignifikanciaszintje
érvényes a valós megoszlásra is. A próba
másodfajú hibája azonban a valós megoszláséhoz
képest nagyobb, azaz a véletlenítési eljárás
alkalmazása csökkenti a függetlenségi próba
erejét.
5. Többdimenziós elemzések
Diszkrét változók függetlenségi modelljeinek vizsgálatára a log-lineáris modellek a legelterjedtebbek. Ezek közül a hierarchikus log-lineáris modellek hibás besorolás melletti vizsgálatára vonatkozó, Korn (1981) által kidolgozott tételt alkalmazhatjuk véletlenített kérdõíves technikával kapott adatokra.
Több változós hierarchikus log-lineáris modellt meghatározhatunk a változók közötti kölcsönhatások rendszerével, vagyis a változók olyan minimális halmazaival, amelyeknek az elemei közötti interakciók a modellben jelen vannak. Korn két feltétel mellett határozta meg a félreosztályozási hibáktól védett log-lineáris modellek csoportját. Az egyik az, hogy a félreosztályozások függetlenek legyenek a változók valós értékeitõl, a másik, hogy az egyes változók mérésekor elkövetett hibák egymástól függetlenek legyenek. Mindkét felvétel a véletlenített kérdezéssel gyûjtött adatokra érvényes. Mint az elõzõ fejezetben látható volt, a hibásan besorolt, és a véletlenített technikával kérdezett adatok egymással ekvivalens módon írhatók fel a valós megoszlások segítségével, így a tétel alkalmazható. Egy hierarchikus log-lineáris modellt akkor nevezünk a d-dik változóban félreosztályozási hibától (és így a véletlenítési eljárás torzító hatásától) védettnek, ha csak a d-dik változóban követtünk el félreosztályozási hibákat, és ha a modell illeszkedési szintje a valós és a megfigyelt eloszlásra megegyezik. Korn tételének véletlenített kérdõíves adatokra való alkalmazása tehát a következõ:
Egy hierarchikus log-lineáris modell akkor és csak akkor védett a d-dik változóban a véletlenítés hatásától, ha a modell minimális halmaza egy és csak egy olyan interakciós tagot tartalmaz, amelynek indexében d elõfordul.
Az A1, A2, A3 változók log-lineáris modellek esetén például a H(13,23) modell illeszkedési jósága megegyezik a megfigyelt adatokra és a valós adatokra, ha az elsõ, és/vagy a második változóra a kérdezés véletlenítéssel történt. A harmadik változóra ez már nem igaz, mivel ennek az indexe kétszer is szerepel a modell minimális halmazaiban. Azok a modellek, amelyek a teljes függetlenséget, vagy egy változónak az összes többitõl való függetlenségét, vagy egymást kölcsönösen kizáró változóhalmazok egymástól való függetlenségét írják le, minden változóban védettek a véletlenítés torzító hatásától.
Ez az eredmény csak arra vonatkozóan ad eligazítást, hogy az adott modell illeszkedését a megfigyelt adatokra elfogadhatjuk vagy sem, a modell paraméterei a valós megoszlásra azonban már nem értelmezhetõk. Ahhoz, hogy a változók közötti asszociáció mértékét becsülhessük, olyan log-lineáris modelleket kell találni, amelyek figyelembe veszik a valós és a megfigyelt eloszlás közötti összefüggést: Ez az összefüggés jelen esetben, diszkrét eloszlás mellett olyan átmenetmátrixszal írható le, amelynek elemei a véletlen kísérlet kimeneteleinek valószínûségeibõl állnak.
Tekintsünk elõször olyan három változós log-lineáris modelleket, ahol a három változó közül kettõnél véletlenített kérdõíves technikával történt kérdezés, a harmadiknál direkt módon. Ezt a helyzetet olyan, öt változós log-lineáris modell segítségével tudjuk leírni, amelyben a két valós eloszlású meg nem figyelt, a két véletlenítéssel megfigyelt, és a direkt módon megfigyelt változók együtt szerepelnek. Legyen a három vizsgálandó változó A, B és C, melyek közül A és B véletlenítéssel lett kérdezve, ezeknek a valós megoszlású megfelelõit jelöljük A'-vel illetve B'-vel. A log-lineáris modellt az A1, B, C, A', B' változókra fogalmazzuk meg.
A véletlenítés általános struktúráját a következõ egyenletekkel lehet felírni:
pijklm=p..klm(pi..k./p...k.) (p.j..m/p....m) (5.1),
ahol i=1,...I, j=1,...J, k=1,...K, l=1...I és m=1,...J,
és azok a cellavalószínûségek, amelyeknek indexeiben pont van, az illetõ változó szerinti marginális tábla cellavalószínûséget jelentik. Jelen esetben, ahol mindegyik véletlenítve kérdezett változó dichotóm, I és J egyenlõ 2-vel. Az (5.1) egyenlet azt írja le, hogy az ötdimenziós tábla celláit a valós megoszlásból oly módon kapjuk, hogy a C, A', B' marginális valószínûséget a feltételes valószínûségekkel, vagyis az átmenetmátrixok elemeivel megszorozzuk, amelyek a véletlenítõ kísérletek kimeneteleinek megoszlását írják le:

ahol 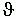 1 és
1 és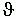 2,
A, illetve B változóra vonatkozó véletlenített
kérdezésnél a negatív kérdés
elõfordulási valószínûsége (ld.
2. táblázat).
2,
A, illetve B változóra vonatkozó véletlenített
kérdezésnél a negatív kérdés
elõfordulási valószínûsége (ld.
2. táblázat).
A fentebb is használt minimális halmazok segítségével a pijklm cellavalószínûségek (5.1) log-lineáris modellje H(14,25,345,) jelöléssel írható le. Ebben a modellben azonban szerepelnek a meg nem figyelt valós eloszlású változók is, viszont megfigyeléseink csak a pijk.. cellavalószínûségû marginális táblára vonatkozóan vannak, míg következtetéseket a p..klm marginális tábláról szeretnénk levonni. Az utóbbi, valós megoszlásra vonatkozó log-lineáris modelleket H*-gal jelöljük, például azt a C, A', B' változókra vonatkozó modellt, amely nem tartalmaz másodrendû interakciót, H*(34,35,45) jelöli. Ez a modell és az (5.1) egyenlettel leírt H(14,25,345) modell log-lineáris rendszerek rekurzív rendszerét alkotják, ami azt jelenti, hogy a változóknak létezik olyan sorszámozása, amely szerint minden változó direkt vagy indirekt okai kisebb sorszámot kapnak, mint maga a változó, és így minden elemzést el lehet végezni rekurzíve úgy, hogy minden sorszámozott változatot az alacsonyabb sorszámúak részhalmazán vizsgálunk (Feinberg 1977; Kiiveri-Speed 1982). Jelen esetben a külsõ (exogén) változók, vagyis az okok az 1-es és 2-es indexû, azaz az A és B változók, míg a belsõ (endogén) változók, azaz az okozatok a 3-as, 4-es és 5-ös, azaz a C, A' és B' változók.
A H(14,25,345) és a H*(34,35,45) modellek mellett a p...klm cellavalószínûségekre kapható maximum likelihood becsléseket a következõ maximum likelihood egyenletek segítségével lehet meghatározni:

ahol pijklm ki kell elégítse (1) egyenlet alapján a

egyenletet.
Az (5.5) egyenletek jobb oldalai a cijk/N relatív
gyakoriságoknak az (i, j, k, l, m) cellákba való
arányos allokációinak összegei, ahol az allokációk
a pijklm becslések alapján történnek.
Az (5.5) és (5.7) egyenletrendszer megoldására Chen
(1979) az arányos iteratív illesztés (IPF) módszerének
(Bishop-Feinberg-Holland 1975) módosított változatát
javasolja, amelyben az IPF algoritmus minden egyes lépésénél,
amikor a kontingencia-tábla valamely belsõ celláját
arányosan módosítjuk úgy, hogy a modell által
elõírt egyes marginálisokhoz illeszkedjen, akkor az
(5.7) egyenletnek megfelelõen is arányosan módosítjuk
a becslést. Miután a pijklm becsléseket
megkaptuk, a modell illeszkedését a Pearson féle statisztika
segítségével ellenõrizhetjük, (IJ-LM)K
szabadság fok mellett. Az algoritmus több változó
kezelésére képes általánosított
változatát a véletlenített és direkt
technikával kérdezett adatok log-lineáris elemzésére
írt programterv (Bornemisza 1995) tartalmazza.
6. A minta
A megkérdezettek kiválasztása során olyan populációt igyekeztünk találni, melynek tagjairól joggal gondolhattuk, hogy van titkolnivalójuk. Számos lehetõség merült föl, mint például alkoholizmus, kábítószerezés, szexuális perverzió, elmegyógyászati kezelés. Nem volt egyszerû ilyen minta létrehozása. Végül a büntetett elõélet mellett döntöttünk. Szabadságvesztésüket letöltött férfiakat kerestünk föl, azonban titokvédelmi okok folytán nem mondtuk meg a kérdezõbiztosoknak, hogy kiket keresnek meg. A kérdezõbiztosok, valamint a megkérdezettek egyaránt úgy tudták, hogy a kérdezés célja az ugyancsak "érzékeny"-nek minõsíthetõ alkoholizmus kérdésével kapcsolatos személyes információk gyûjtése.
A büntetett elõéletû személyek megkeresése
a gyakori címváltozás miatt számos akadályba
ütközött. A próbakérdezés csökkentette
a minta elemszámát. További elemszám csökkentõ
tényezõ volt, hogy csak azoknak a megkérdezetteknek
a válaszait dolgoztuk fel, akik a kérdezõbiztosok
kérdõíven utólag rögzített beszámolói
szerint megértették a meglehetõsen bonyolult kérdezési
eljárást, és a kérdezési utasításoknak
megfelelõen válaszoltak a kérdõív kérdéseire.
A vizsgálatban ily módon 35 olyan személy vett részt,
akikrõl biztosan tudhattuk, hogy az "érzékeny" kérdés
számukra valóban az. Kiegészítésként
140 személyt vettünk fel a mintába, akiknek az életkor,
lakóhely és iskolai végzettség szerinti megoszlása
ugyanolyan, mint az "érzékeny"-ek mintájában.
7. A kérdõív
A próbakérdezés során két véletlenítési eljárással kísérleteztünk. Az egyik a 2. pontban említett "erõltetett alternatíva". A kérdezett olyan kártyacsomagot kapott, amelyben háromféle utasítást talált, mindegyiket külön lapon. A kártyacsomag megkeverése után húznia kellett. Az egyik típusú kártyán azt az utasítást találta a kérdezõ, hogy feltétlen igennel válaszoljon, a másikon azt, hogy feltétlen nemmel, a harmadik típusú kártya utasítása szerint a válaszadónak nyíltan válaszolnia kellett a feltett kérdésre.
A másik eljárás Warner nevéhez fûzõdik. A megkérdezettnek itt is egy tíz lapból álló kártyacsomagot adnak át, amelyet össze kell kevernie. Ezt követõen húzhatja ki a kártyát. Ez a módszer csak kétféle kártyát ismer. Az egyiken a kérdésre adható válasz állító megfogalmazása található ("Igaz-e, hogy Ön volt már..."), a másikon a válasz tagadó megfogalmazása ("Igaz-e, hogy Ön soha nem volt...").
A próbakérdezésnél, amelyet az eredetileg rendelkezésre álló büntetett elõéletûek mintájából választott személyekkel végeztünk, azt kellett tapasztalnunk, hogy az erõltetett alternatíva módszere nem vált be. A válaszadók kiléptek a kérdezési szituációból, és mintegy "bevallották", hogy a valóságos helyzet más, mint amire az utasítás vonatkozik.
E tapasztalatok birtokában úgy döntöttünk, hogy a Warner-féle módszert választjuk.
A kérdezõbiztosok azzal a kéréssel keresték meg a megkérdezetteket, hogy válaszoljanak egy az alkoholizmussal kapcsolatos kérdõívre. Ennek megfelelõen a bevezetõ 14 kérdés az alkoholizmussal kapcsolatos attitûdökre és személyes problémákra vonatkozott.
Ezt követõen kezdõdtek a véletlenített kérdezés módszerei szerint feltett kérdések. Figyelmeztettük a megkérdezetteket arra, hogy a módszer bonyolult, gyakorlást igényel. Az állítottuk, hogy két gyakorló kérdés lesz. Valójában csak az elsõ kérdés volt gyakorló jellegû:
Igaz-e hogy Ön kipróbált már valamilyen
kábítószert (hat kártyán )
Igaz-e, hogy Ön soha nem fogyasztott kábítószert
(négy kártya)
Mindegyik esetben a válaszadó igen-nel vagy nem-mel válaszolhatott.
A második kérdéspárról is azt állítottuk, hogy gyakorló célokat szolgál, de valójában ez volt az az érzékeny kérdés, melyre vonatkozólag a válaszokra tényleg kíváncsiak voltunk. Azért állítottuk errõl a kérdésrõl is, hogy az gyakorló, mert így próbáltuk a megkérdezettek figyelmét elterelni, esetleges gyanakvását elaltatni.
Igaz-e, hogy Ön volt már szabadságvesztésre
ítélve? (hat kártya)
Igaz-e, hogy Ön soha nem volt szabadságvesztésre
ítélve? (négy kártya)
Ezt követõen még két kérdést
tettünk fel hasonló módszerrel. A megkérdezettek
(és a kérdezõbiztosok) ugyan azt hitték, hogy
ezek a valódi érzékeny kérdések, de
valójában csak az álcázást szolgálták.
(Volt-e már alkoholelvonó kúrán? Elõfordult-e
már, hogy Ön ittas állapotban bántalmazta valamelyik
családtagját?)
8. Eredmények
Mint már említettük, az adatok feldolgozása során csak azokat a kérdõíveket vettük figyelembe, amelyek végén a kérdezõ a két ellenõrzõ kérdésre olyan értékeléseket adott, amelyek alapján feltételezhettük, hogy a megkérdezett megértette a kísérlet célját, és az utasításnak megfelelõen válaszolt. A szûrést követõen a kísérleti mintából 4-en, a kontroll-mintából 9-en estek ki. Ily módon az általunk vizsgált minta létszáma 163 lett (kísérleti minta 32, kontroll-minta 131).
3. táblázat
A teljes minta válaszainak megoszlása az "érzékeny"
kérdésre
|
|
|
|
|
|
|
|
|
|
|
|
Ezeknek az adatoknak az alapján számolva, a valós igen válaszok gyakoriságának becslése (3.5) alapján 27 százalék Ez a szám 6,8 százalékkal magasabb, mint a büntetett elõélet általunk biztosan tudott tényleges elõfordulása. Kereszttáblával megnéztük, hogy az általunk biztosan tudott büntetett elõéletûek válaszai miként különböznek a kiegészítõ minta válaszaitól.
4. táblázat
A büntetett elõéletûek válaszai
|
|
|
|
|
|
|
|
|
|
|
|
A táblázatból látható, hogy az általunk biztosan tudott büntetett elõéletûek nem csaltak. A véletlenített kérdezés módszerével sikerült elhárítani a hamis válasz adásának kísértését. A módszer tehát jól mûködött. A táblázat egyben azt is sejteti, hogy a teljes mintán kapott eltérés a kiegészítõ minta tagjainak válaszaira vezethetõ vissza.
5. táblázat
A kiegészítõ minta válaszai
|
|
|
|
|
|
|
|
|
|
|
|
A kiegészítõ minta tagjai körében azt tapasztaltuk, hogy a várható 40:60 arányhoz képest a kapott arány 41:58.
Az igen-nel válaszolók várthoz képest magasabb aránya azzal magyarázható, hogy a kontroll-mintába véletlenszerûen bekerülhettek büntetett elõéletûek. Ez annál is inkább valószínûsíthetõ, mivel szociológiai és demográfiai szempontból a kontroll minta mintegy a kísérleti minta tükörképe volt. (A kis elemszám miatt egy büntetett elõéletû személy bekerülése is elég.)
A kontroll-minta esetében u próbát végeztünk.
Az u próba arra szolgál, hogy a megfigyelt eloszlás
illeszkedését vizsgálja az elméleti eloszláshoz
képest. Az elméleti megoszlás jelen esetben 60:40
százalék, azaz a kártyacsomagban eleve megadott pozitív-negatív
kérdések közötti arány. Az u próba
értéke 3,2, ami azt jelenti, hogy a megfigyelt eloszlás
elfogadható szinten illeszkedik a valós eloszláshoz.
A kísérleti mintában az u próba értéke
1,6 volt, ami nagyon jó illeszkedésre utal.
Diszkusszió
A vizsgálat eredményei azt mutatják, hogy sikeresen operacionalizáltuk az érzékenység dimenzióját. Továbbá, az is bebizonyosodott, hogy az általunk választott véletlenített kérdezési módszer alkalmas érzékenynek minõsülõ kérdések vizsgálatára, és számottevõen mérsékelni tudja a bizalmatlanságból, konformitásból, ön-prezentációs feszültségekbõl adódó õszinteség-hiányt.
A vizsgálat eredményei alapján azt mondhatjuk, hogy a véletlenített kérdezés módszerével érvényes válaszok kaphatók.
A módszer korlátai elsõsorban azzal függnek
össze, hogy nehezen érthetõ. Másodsorban az is
nyilvánvaló, hogy jóval több idõt vesz
igénybe, mint a szabvány kérdezési mód.
Nem kétséges, hogy a szokásos közvélemény-kutatások
esetében a feltett kérdések csak a minta egy kis része
számára számítanak igazán érzékenynek.
Ez az arány azonban nem olyan magas, hogy veszélyeztetné
a teljes mintára kapott adatok hitelét. Következésképpen
reprezentatív mintán végzett szokásos (piackutatással
foglalkozó, politikai, választási attitûdöket
felmérõ stb.) közvélemény-kutatások
esetében alkalmazható ugyan a véletlenített
kérdezés módszere, de nem éri meg a fáradságot.
Ezzel szemben lehetnek olyan speciális programok, melyek megtervezése,
elõkészítése során szükség
van ilyen módszerek alkalmazására, ahhoz, hogy érvényes
és megbízható válaszokat kapjunk. Egyes esetekben
a speciális érzékenység a társadalom
széles köreire is kiterjedhet, elég ha az adózásra,
nemi életre gondolunk. Ilyenkor a véletlenített kérdezés
módszere akár reprezentatív mintán is alkalmazható.
Hivatkozások
Angelusz R. 1997. Optikai csalódások. Budapest: Pesti Szalon
Angelusz R.-S. Molnár E. 1976. A közvélemény-kutatás néhány ismeretelméleti-módszertani problémája. In: Szociálpszichológiai kutatások Magyarországon. Budapest: Akadémiai Kiadó
Angelusz, R.-Csepeli Gy.-Kulcsár L.-S. Molnár E. 1975. A kommunikáció folyamata és a vélemények alakulása. Budapest: Tömegkommunikációs Kutatóközpont
Assakul, K.-C. H. Proctor 1967. Testing Independence in Two-Way Contingency Tables with Data Subject to Misclassification. Psychometrika, (vol. 32) 1, 67-76.
Bishop, Y. M. M.-S. E. Feinberg-P. W. Holland 1975. Discrete Multivariate Analysis. Cambridge, London: MIT Press
Bornemisza E. 1994. Hibával mért statisztikai adatok elemzése. Társadalomkutatási Módszertani Kiadványok. A mérés problémája a társadalomtudományokban 2. Budapest: TÁRKI-OMIKK
- 1995. Programterv véletlenített kérdõívvel és direkt módon kérdezett változók log-lineáris elemzésére. TÁRKI preprint, 2.
Bradburn, N. M.-S. Sudman 1979. Improving Interview Method and Questionnaire Design. San Francisco: Jossey-Bass
Bross, I. 1954. Misclassification in 2x2 Tables. Biometrics, vol. 10, 478-486.
Chen, T. T. 1979. Analysis of Randomized Response as Purposively Misclassified Data. Proceedings of the Survey Research Methods Section, ASA
Cohran, W. G. 1968. Errors in Measurement in Statistics. Technometrics, (vol. 10), 4, 637-666.
Csepeli Gy. 1978. Kísérlet a szomszéd népek iránti attitûdök közvéleménykutatási eszközökkel való megragadására. TK Mûhely, (IX. évf.) 24.
Feinberg, S. E. 1977. The Analysis of Cross-classified Categorical Data. Cambridge, Massachusetts: MIT Press
Folsom, R. E. et al. 1974. The Two Alternate Questions Randomized Response Model for Human Surveys. JASA, vol. 68, 525-530.
Fox, J. A.-P. E. Tracy. 1987. Randomized Response. Sage.
Kiiveri, H.-T. P. Speed 1982. Structural Analysis of Multivariate Data: a Review. Sociological Methodology, 3.
Koch, G. G. 1969. The Effect of Non-sampling Errors on Measures of Association in 2x2 Contingency Tables. JASA, vol. 64, 852-863.
Korn, E. L. 1981. Hierarchical Log-linear Models Not Preserved by Classification Error. JASA, vol. 76, 110-113.
Moors, J. J. A. 1971. Optimization of the Unrelated Question Randomized Response Model. JASA, vol. 66, 627-629.
Rudas T. 1979. Véletlenített kérdõíves eljárások. TK Mûhely, (X. évf.) 17.
Stem, D. E.-R. K. Steinhorst. 1984. Telephone Interview and Mail Questionnaire Applications of the Randomized Response Model. JASA, vol. 79, 555-564.
Tenenbein, A. 1970. A Double Sampling Scheme for Estimating from Binomial Data with Misclassification. JASA, vol. 65, 1350-1361.
Tóth I. J. 1997. Az adófizetõk jövedelemszerkezete és adótehermegoszlása 1996-ban. TÁRKI Társadalompolitikai tanulmányok, 2.
Warner, S. L. 1965. Randomized Response: A Survey Technique for Eliminating
Evasive Answer Bias. JASA, vol. 60, 63-69.
* Köszönetet mondunk Rudas Tamásnak értékes közremûködésééért. A kutatást a T 13699 számú OTKA program támogatta.