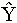 a függõ változó
becsült értéke,
a függõ változó
becsült értéke, 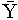 , illetve
, illetve  a függõ, illetve a magyarázó változó
átlaga, b1 pedig a magyarázó változó
hatását kifejezõ standardizálatlan regressziós
együttható:4
a függõ, illetve a magyarázó változó
átlaga, b1 pedig a magyarázó változó
hatását kifejezõ standardizálatlan regressziós
együttható:4
"Ezeknek az illeszkedési mutatóknak végzetes vonzerejük van. Bár a hozzáértõk rendszerint elismerik, hogy semmit sem jelentenek, magas értékeik mégis büszkeséggel és elégedettséggel töltik el létrehozóikat, bármennyire igyekeznek is titkolni ezeket az érzéseiket" (Cramer 1987: 253).
Kevés statisztikai mutató örvend akkora népszerûségnek
és tiszteletnek a társadalomkutatók körében,
mint a determinációs együttható. Az R2
úgyszólván kötelezõ tartozéka minden
valamirevaló tudományos publikációnak, és
sokan szinte megszállottként törekednek a növelésére.1
Olyan mutató is kevés akad azonban, amelyet gyakrabban használnának
fölöslegesen vagy éppen hibásan, és amelyhez
több téves értelmezés, megalapozatlan várakozás
tapadna. Ennek az írásnak a célja a determinációs
együttható értelmezésével és alkalmazásával
kapcsolatos néhány probléma áttekintése.
A kutatás célja és a determinációs együttható szerepe
Az R2 kiszámítása és közlése úgyszólván reflexszerû eljárás a legtöbb kutatónál és eközben rendszerint fel sem merül a kérdés: indokolt-e egyáltalán a mutató használata. A válasz erre a kérdésre alapvetõen függ a kutatás céljától. Amennyiben a vizsgálat valamely jelenség elõrejelzésére irányul, akkor nyilvánvalóan nem mellékes, hogy a magyarázó változó alapján mennyire pontosan tudjuk meghatározni a függõ változó értékét; mennyire tudjuk leszorítani a becslési vagy elõrejelzési hibát. Ilyenkor valóban indokolt lehet a determinációs együttható figyelembevétele, az R2 ugyanis többnyire arra utal, hogy a függõ változónak a magyarázó változó ismeretében megjósolt értéke kevéssé tér csak el a ténylegestõl, vagyis a becslési hiba viszonylag csekély.2 Hamarosan látni fogjuk azonban, hogy az R2 nagysága nem csupán e hiba mértékétõl függ, s ezért ez a mutató csak korlátozottan alkalmas az elõrejelzés sikerességének mérésére.
Alapvetõen más a helyzet, ha a kutatás célja
elméleti magyarázat ellenõrzése. Ilyenkor
rendszerint tapasztalati következményeket fogalmazunk meg;
olyan várakozásokat, amelyek azt fejezik ki, miként
kell kinéznie a világnak akkor, ha az általunk kidolgozott
magyarázat valóban igaz. Ha például annak az
elképzelésnek a helyességét vizsgáljuk,
amely szerint a neurózisnak a nõk körében tapasztalt
nagyobb gyakoriságáért a két nem eltérõ
társadalmi szerepei, a nõknek a nemek közötti munkamegosztásból
eredõ nagyobb leterheltsége a felelõs, akkor ésszerûnek
látszik arra számítani, hogy a férfiak és
a nõk lelki egészségi állapota városban
kevésbé tér el egymástól, mint falun,
hiszen a nemi szerepek, a nemek közötti munkamegosztás
városban minden bizonnyal kiegyenlítettebb, mint vidéken.
Ez a várakozás vagy tapasztalati következmény
- és számunkra ez most a fontos - három változó
összefüggését, egymásra hatását
írja le: nevezetesen azt, hogy a nem hatása a neurózisra
függ a település típusától. Márpedig
egy változó másikra gyakorolt hatását
- e hatás nagyságát és irányát
- a standardizálatlan regressziós együttható
tükrözi; a determinációs együttható
értéke ebbõl a szempontból teljesen közömbös.3
Egy alacsony R2 legfeljebb arra utal, hogy a függõ
változót az általunk vizsgált magyarázó
változón kívül még egy sereg más
tényezõ is befolyásolja; ez azonban lényegtelen,
hiszen bennünket egy meghatározott oksági kapcsolat
érdekel, s nem arra a lehetetlen, egyszersmind fölöttébb
kétes értékû feladatra vállalkoztunk,
hogy teljes körû leltárt készítsünk
valamely jelenség okairól.
Az R2 és a "magyarázó erõ"
A determinációs együtthatóról gyakran állítják, hogy a regressziós modell - illetve az abban szereplõ változók - magyarázó erejét fejezi ki. Ez a megfogalmazás kétségkívül jól hangzik (sokak számára éppen ezért igen vonzó), azonban meglehetõsen félrevezetõ, ugyanis összekeveri egymással a statisztikai és a tartalmi magyarázatot. Statisztikai értelemben megmagyarázni valamit annyit jelent, hogy a függõ változó teljes szóródásának minél nagyobb hányada esik a magyarázó változó egyes értékei vagy kategóriái közé, és minél kisebb hányada marad ezeken az értékeken vagy kategóriákon belül. Ebben a tisztán statisztikai értelemben az R2 valóban a "megmagyarázott variancia" nagyságát jelzi; ennek azonban az égvilágon semmi köze a vizsgált jelenség tartalmi magyarázatához. Gondoljuk csak meg: ha magyarázó változóként magát a függõ változót használnánk, akkor az R2 garantáltan a lehetõ legnagyobb, éspedig 1 lenne, vagyis a függõ változó teljes szóródását meg tudnánk "magyarázni". Mégis, aligha mondaná bárki, hogy ezáltal akár csak egyetlen lépéssel is közelebb jutottunk a vizsgált jelenség megértéséhez, tartalmi értelemben vett magyarázatához (lásd Lewis-Beck 1993: 16; King 1986: 677).
Az, hogy a determinációs együttható azonosítása a magyarázó erõvel mennyire téves lehet, azt az immáron klasszikusnak mondható tankönyvi példával is érzékeltethetjük. A születések száma egy adott településen elég nagy pontossággal megbecsülhetõ a házak kéményein fészkelõ gólyák száma alapján; ha lefuttatunk egy regressziót, amelyben a magyarázó változó a gólyák száma, a függõ változó pedig a születések száma, akkor az R2 értéke valószínûleg meglehetõsen magas lesz. De következik-e ebbõl, hogy a gólyák száma magyarázza - tartalmi értelemben - a termékenység szintjét? Nyilvánvalóan nem; statisztikai magyarázó erejét - ami a magas R2-ben tükrözõdik - ez a változó kizárólag annak köszönheti, hogy erõsen korrelál a születésszám valódi meghatározójával, a település típusával. Falun egyrészt gyakoribb a gólya, mint városban, másrészt itt a termékenység is eleve magasabb.
Vegyük észre, hogy pusztán az elõrejelzés szempontjából ez a probléma voltaképpen nem probléma: ebben a tekintetben tökéletesen mindegy, hogy a magyarázó változó valóban oka-e a függõ változónak, vagy az összefüggés látszólagos csupán (Cook-Campbell 1979: 296-297; Elster 1997: 18). Sõt, mivel a valódi oksági tényezõk gyakran nehezebben mérhetõk, mint a velük korreláló egyéb változók, tisztán gyakorlati megfontolásból ez utóbbiak alkalmasint még hasznosabbak is lehetnek. Egészen más a helyzet, ha nem elõrejelzésrõl, hanem magyarázatról van szó. Ekkor már távolról sem közömbös, mi húzódik meg a nagy R2 mögött: tényleges oksági hatás vagy hamis kapcsolat. Ennek megfelelõen ekkor már nagyon is tudatában kell lenni annak, hogy a determinációs együttható magas értéke egyáltalán nem feltétlenül utal valódi oksági magyarázatra.
Még egy dolgot érdemes megemlíteni ezen a ponton. A determinációs együtthatót gyakran használják a változók relatív - egymáshoz viszonyított - magyarázó erejének megállapítására. Ez az alkalmazás rendszerint - bár nem szükségszerûen - a lépésenkénti regresszióhoz kötõdik; olyan eljáráshoz, ami - ha lehet - még kétesebb értékû, mint az R2 nyakló nélküli növelése. A lépésenkénti regresszió általában annak alapján állít fel fontossági sorrendet az egyes magyarázó változók között, hogy milyen mértékben járulnak hozzá a determinációs együttható növeléséhez. Ezzel nem is volna különösebb baj, ha a magyarázó változók függetlenek lennének egymástól; ekkor ugyanis minden változóhoz egyértelmûen hozzá lehetne rendelni azt az R2-növekményt vagy "magyarázó erõt", ami kizárólag neki tulajdonítható. A gyakorlatban azonban a magyarázó változók rendszerint többé-kevésbé erõsen korrelálnak egymással. Ebben az esetben a "magyarázó erõt" már nem lehet egyértelmûen hozzárendelni az egyes változókhoz; túl azon a mértéken, ami minden változót a "saját jogán" megillet, van egy olyan rész is, ami közös, ami egyiknek sem kizárólagos "tulajdona". Az, hogy ezt a közös "magyarázó erõt" melyik változó kapja meg, a változók bevonásának sorrendjétõl függ: az a változó, amely elsõként kerül be a modellbe, saját részén kívül "magával viszi" ezt a közös részt is, és így aránytalanul fontosnak, jelentõsnek látszik; annak a változónak pedig, amelyet másodikként vonunk csak be, a közös részbõl már semmi sem marad, és így a ténylegesnél kevésbé fontosnak tûnik. Korreláló magyarázó változók esetén tehát az R2-növekmény mértéke nem használható annak megítélésére, melyik változó fontosabb, melyiknek nagyobb a "magyarázó ereje", ez ugyanis teljes egészében attól függ, milyen sorrendben vonjuk be õket az elemzésbe. (Minderrõl bõvebben lásd Lewis-Beck 1978; Pedhazur 1982: 167-171; Kennedy 1992: 63-64.)
Hogy mennyire hibás következtetésekhez vezethet,
ha az R2-növekmény alapján foglalunk állást
egy változó súlyáról, szerepérõl,
azt a gólyákkal és a születések számával
kapcsolatos iménti példával is érzékeltethetjük.
Tegyük föl, hogy a termékenység szintjét
két, egymással korreláló változóval:
a gólyák számával és a település
típusával próbáljuk megmagyarázni, és
arra vagyunk kíváncsiak, e két tényezõ
közül melyik a fontosabb. Tegyük föl továbbá,
hogy valamilyen oknál fogva - mondjuk, apró mérési
hiba vagy más ehhez hasonló jelentéktelen dolog miatt
- a gólyák száma hajszálnyival erõsebben
korrelál a termékenységgel, mint a másik magyarázó
változó, a település típusa. Ebben a helyzetben
valószínûleg a gólyák száma kerül
be elsõként a modellbe - hiszen a beválasztás
szempontja az elsõ szakaszban általában a függõ
változóval való egyszerû korreláció
mértéke -, magával vive annak a közös "magyarázó
erõnek" a teljes egészét is, amely pedig részben
a másik változót, a településtípust
illetné meg. Ez utóbbi változónak így
aztán már semmi sem marad a közös "magyarázó
erõbõl", és ennek megfelelõen kevésbé
fontosnak, kisebb "magyarázó erejûnek" látszik.
Történik mindez annak ellenére, hogy oksági szempontból
nyilvánvalóan épp a településtípus
a fontos, és a gólyák száma a lényegtelen.
Ha tehát pusztán az R2-növekmény alapján
döntünk, akkor kihagyjuk a valódi oksági tényezõt,
és bevonjuk azt a változót, amelynek a hatása
látszólagos csupán.
Az R2 és az "illeszkedés szorossága"
Másik gyakori nézet szerint a determinációs együttható a regressziós modell illeszkedését méri; azt, hogy a regresszió segítségével a függõ változó értékére adott becslések mennyire esnek közel a tényleges értékekhez; vagy - képszerûbben fogalmazva - hogy az adatpontok mennyire "simulnak rá" a regressziós egyenesre. Láttuk, hogy bár olyan vizsgálatokban, amelyek elméleti magyarázat ellenõrzésére irányulnak, ennek a dolognak nincs túl nagy jelentõsége, azokban a kutatásokban, amelyeknek célja az elõrejelzés, nem lényegtelen a becslések pontossága. Ilyen esetben tehát valóban szükség lehet az illeszkedés valamiféle mutatójára, kérdés azonban, az R2-e a legalkalmasabb erre a feladatra.
Az általános vélekedéssel ellentétben
a determinációs együttható csak korlátozottan
használható a regressziós modell illeszkedésének
mérésére. E mutató értéke ugyanis
nem csupán attól függ, mennyire szorosan tömörülnek
az adatpontok a regressziós egyenes körül - vagyis mennyire
kicsi a becslési hiba -, hanem attól is, mekkora a magyarázó
változó szórása. Ugyanolyan illeszkedés
nagyobb R2-et eredményez, ha a magyarázó
változó értékei szélesebb sávban
szóródnak. A szórásnak ez a hatása
világosan kitûnik az alábbi egyenlõségbõl,
amelyben 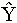 a függõ változó
becsült értéke,
a függõ változó
becsült értéke, 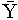 , illetve
, illetve  a függõ, illetve a magyarázó változó
átlaga, b1 pedig a magyarázó változó
hatását kifejezõ standardizálatlan regressziós
együttható:4
a függõ, illetve a magyarázó változó
átlaga, b1 pedig a magyarázó változó
hatását kifejezõ standardizálatlan regressziós
együttható:4
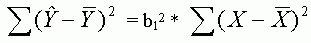 (1)
(1)
Látható, hogy a regressziónak tulajdonítható eltérésnégyzet-összeg - ami a bal oldalon szerepel, s ami nem más, mint a determinációs együttható számlálója - függ a magyarázó változó szóródásától, ami a jobb oldalon áll. Feltéve, hogy b1 értéke nem módosul, minél szélesebb sávban szóródnak az X értékek, annál nagyobb a regressziónak tulajdonítható eltérésnégyzet-összeg, és így - amennyiben a reziduális eltérésnégyzet-összeg állandó - annál nagyobb az R2 értéke is.
Túl a tisztán matematikai bizonyításon, érdemes ezt a kérdést a kutatási gyakorlat oldaláról is szemügyre venni. A társadalomtudományokban viszonylag ritkán adódik alkalom kísérletezésre, a magyarázó változó aktív befolyásolására; rendszerint kénytelenek vagyunk beérni a passzív megfigyeléssel, a változó tõlünk függetlenül kialakult értékeinek puszta feljegyzésével. A mintavétel révén olykor mégis lehetõségünk van arra, hogy a magyarázó változó eloszlását módosítsuk. Ezt tesszük például akkor, amikor szándékosan olyan eseteket vonunk be az elemzésbe, amelyek a magyarázó változó szélsõ pontjait képviselik, vagy amikor egy dichotóm magyarázó változó kategóriáiból azonos számú esetet választunk ki. Mindezek a mintavételi "trükkök" növelik a magyarázó változó szórását5, ezen keresztül pedig a determinációs együttható értékét.
A mintavételnek ezt a hatását jól szemléltetik Blalock (1964: 114-124), Ezekiel és Fox (1970: 18. fejezet), valamint Weisberg (1985: 74-76) munkái, amelyekben a szerzõk mesterségesen módosítják a magyarázó változó szórását, majd megvizsgálják, miként befolyásolja ez a különbözõ statisztikai mutatók értékét. Ez a fajta szimuláció vagy módszertani kísérlet azért is tanulságos, mert rávilágít arra, hogy miközben az R2 értéke számottevõen ingadozik aszerint, hogy széles sávban szóródnak a magyarázó változó értékei, addig a reziduumok szórása - a regressziós becslés standard hibája - nagyjából állandó marad. Ez utóbbi mutató tehát nem függ szisztematikusan a magyarázó változó szórásától6, és így a determinációs együtthatónál alkalmasabbnak tûnik a regressziós modell illeszkedésének, a becslési hiba nagyságának a mérésére.7 A reziduális szórás további elõnye, hogy az illeszkedés "jóságát" a függõ változó természetes mértékegységében fejezi ki - ellentétben az R2 -tel, ami dimenzió nélküli mutató, és ezért általában nehezebben kapcsolható közvetlenül a vizsgált jelenséghez (Achen 1982: 61-64).
Eddig arról beszéltünk, hogy amennyiben a mintavétel
folyamán képesek vagyunk mesterségesen növelni
a magyarázó változó szórását,
akkor a determinációs együttható szinte tetszõlegesen
változtatható; épp ezért ilyenkor rendkívül
körültekintõnek kell lenni e mutató értelmezésekor.
Indokolt lehet azonban az óvatosság fordított esetben
is. Gyakori jelenség, hogy a magyarázó változó
szórása éppenséggel túl alacsony, és
nincs lehetõség a növelésére. Ez a helyzet
akkor, ha a magyarázó változó ritka elõfordulású
eseményre vonatkozik, például arra, hogy a vizsgált
személy követett-e el fiatal korában öngyilkossági
kísérletet vagy súlyosabb bûncselekményt.
Az ilyen személyek a teljes mintának vélhetõleg
viszonylag csekély hányadát képezik csupán,
vagyis - technikailag kifejezve - a magyarázó változó
eloszlása meglehetõsen ferde: az esetek zöme az egyik
kategóriában összpontosul, és a másik
kategóriába csak kevés megfigyelés tartozik.
Ennek következtében a magyarázó változó
szórása viszonylag kicsi lesz, hiszen egy dichotóm
változó varianciája egyenlõ a két kategória
relatív gyakoriságának a szorzatával. Minél
eltérõbbek a relatív gyakoriságok - minél
ferdébb a változó eloszlása -, annál
kisebb a szorzat értéke, azaz annál csekélyebb
a szórás. Ritka események hatásának
vizsgálatakor tehát a determinációs együttható
értéke különösen csalóka lehet: a hatás
- amit a standardizálatlan regressziós együtthatóval
vagy annak megfelelõ más mutatóval mérhetünk
- nagy lehet annak ellenére, hogy az R2 viszonylag alacsony
(errõl bõvebben lásd Glenn-Shelton 1983).
Az R2 és a "tökéletes modell"
Gyakran találkozhatunk azzal a nézettel, miszerint a determinációs együttható a regressziós modell "tökéletességét" vagy "teljességét" jelzi. Minél magasabb az R2 értéke, annál jobb - úgymond - a modell; annál hívebben tükrözi a tényleges összefüggéseket. Valóban, sok kutató egyfajta minõségtanúsító pecsétként kezeli a determinációs együtthatót; olyan védjegyként, amely önmagában szavatolja az elvégzett munka értékét, a felállított modell helyességét. Ez a felfogás azonban alapvetõen téves, az a törekvés pedig, ami ebbõl a felfogásból fakad, és ami az R2 mindenáron való növelésére irányul, teljesen értelmetlen. Elõször is, tökéletes modell nincs; nem azért, mert a tökéletesség elérhetetlen, hanem azért, mert a modell definíció szerint a valóság leegyszerûsített és így szükségképpen pontatlan képe (King 1991: 1048). Olyan kép, amely bizonyos részeket tudatosan kiemel, felnagyít, másokat viszont szándékosan árnyékban hagy. Minden modell meghatározott elméleten nyugszik és ennek az elméletnek a hangsúlyait tükrözi. És minden modell csak egy másik, a sajátunkéval versengõ elmélet talajáról bírálható; nem pedig annak alapján, hogy az R2 értéke túlságosan alacsony. Amikor a regressziós egyenletet újabb változókkal bõvítjük, a cél nem a determinációs együttható növelése; nem valamiféle teljes vagy végsõ modell elérése, hanem a különféle alternatív magyarázatok kiküszöbölése (Achen 1982: 52). Az, hogy valamely modell jó vagy rossz, elméleti érveléssel dönthetõ csak el; az R2 -nek ebbe nincsen beleszólása. Baj is volna, ha lenne; ha gépies számításokkal lehetne pótolni a tartalmi gondolkodást.
Azt a tényt, hogy a regressziós modell "jósága" mennyire nem a determinációs együttható értékén múlik, egy példával érzékeltethetjük. Tegyük föl, hogy olyan képzési program hatékonyságát vizsgáljuk, amelynek célja a munkanélküliek elhelyezkedésének az elõsegítése. Tegyük föl továbbá, hogy a részvétel a programban önkéntes: azok az állástalanok, akiket érdekel a dolog, igénybe veszik a felkínált lehetõséget, a többiek pedig kimaradnak belõle. A két csoportot összehasonlítva megállapítjuk, hogy azok, akik részt vettek a képzésben, átlagosan rövidebb idõ alatt találtak újra munkát, mint azok, akik nem vettek részt. Tudjuk persze, hogy épp az önkéntesség miatt ez az eredmény nem bizonyítja a képzés hatékonyságát: elképzelhetõ, hogy azok, akik a részvétel mellett döntöttek, eleve jobban törekedtek az újbóli elhelyezkedésre, s így a program nélkül is könnyebben találtak volna állást. Az is lehetséges, hogy a résztvevõk fiatalabbak és iskolázottabbak - vagyis olyan tulajdonságokkal rendelkeznek, amelyek önmagukban megkönnyítik az elhelyezkedést. Ahhoz, hogy a képzés tényleges hatását megállapítsuk, mindezeket a tulajdonságokat kontrollváltozóként be kell vonni az elemzésbe. Ezzel azonban - a magyarázó változók körének kibõvítésével - egyszersmind a determinációs együttható értékét is minden valószínûség szerint jócskán megnöveljük, vagyis modellünk - pusztán az R2 nagysága alapján ítélve - igencsak jónak látszik.
Képzeljük most el, hogy a részvétel a programban nem önkéntes, hanem randomizálást alkalmazva a véletlenre bízzuk annak eldöntését, hogy az állástalanok közül ki kerül a képzésben részesülõk csoportjába. Ebben az esetben a programban részt vevõk és az abból kimaradók összetétele minden lehetséges szempontból nagyjából azonos lesz - körülbelül ugyanannyi lesz a fiatalok és az idõsek, az iskolázottak és az iskolázatlanok aránya, és ugyanígy durván azonos lesz azoknak az aránya, akik eleve nagyobb igyekezettel próbálnak elhelyezkedni. Mi következik ebbõl? Az, hogy a program tényleges hatásának megállapítása szempontjából ezúttal nincs szükség a korábban használt kontrollváltozókra, hiszen most sem az életkor, sem az iskolázottság, sem semmilyen más tulajdonság nem korrelál a képzésben való részvétellel.8 Ez azonban - a kontrollváltozók kihagyása - egyszersmind azt is jelenti, hogy az R2 értéke valószínûleg lényegesen alacsonyabb lesz, mint az elõzõ esetben, amikor maguk a munkanélküliek döntötték el, részt vesznek-e a programban. De vajon mondhatjuk-e azt ennek alapján, hogy ez a második modell rosszabb, kevésbé "tökéletes", mint az elsõ? Aligha; sõt, minden bizonnyal épp az ellenkezõje az igaz, hiszen az oksági összefüggések feltárása szempontjából a randomizált vizsgálatoknál nehéz tökéletesebbet elképzelni.
A nagy R2 azonosítása a "tökéletes" modellel egy másik szempontból is alapvetõen hibás. A determinációs együttható növelésének lázában a kutatók a regressziós modellt gyakran az adatpontok véletlenszerû ingadozásaihoz illesztik (Kennedy 1992: 70), figyelmen kívül hagyva, hogy minden adathalmaz csupán minta, egyike a számtalan lehetséges adathalmaznak. Ha történetesen másik adathalmazt figyeltünk volna meg, akkor - a véletlen szeszélye folytán - az adatpontok eloszlása némileg más képet mutatna, és ehhez az eloszláshoz már aligha illeszkedne ugyanolyan jól a modellünk. Akkor hát keressünk másik modellt, ami ehhez az adathalmazhoz hibátlanul illeszkedik? De még újabb mintához már ez a modell sem illeszkedne teljesen - és így tovább a végtelenségig. Nem sokat ér az a "tökéletes" modell, az a nagy R2 , ami csak egyetlen konkrét mintára érvényes. A modell illesztése során mindig csak addig a mértékig érdemes teljességre, tökéletességre törekednünk, ameddig az adatpontok még a vizsgált jelenségben rejlõ törvényszerûséget tükrözik - azt, ami mintáról mintára nagyjából állandó -, nem pedig a puszta esetlegességet, a véletlen ingadozást. Ez is csak azt a régi bölcsességet igazolja, hogy a kevesebb néha több.
Ezt a bölcsességet hagyják figyelmen kívül egyebek között azok, akik sportot ûznek a minél pontosabb görbeillesztésbõl. Õk nem elégszenek meg az egyenessel, hanem másodfokú görbével próbálkoznak; majd a másodfokú görbét felcserélik harmadfokúra; aztán a harmadfokút egy negyedfokúra; míg végül eljutnak az n-1-ed fokú görbéig, amely az n számú adatpont mindegyikén átmegy, vagyis tökéletes illeszkedést, csodálatosan magas R2-et nyújt - csak éppen teljesen értelmetlen, mivel kizárólag az adott mintát, az éppen megfigyelt n esetet képviseli, és így semmi értéke nincs "annak az összefüggésnek a feltárásában, amely valószínûleg érvényes abban a sokaságban, amelybõl a mintában szereplõ megfigyeléseket vettük" (Ezekiel-Fox 1970: 119; lásd még Lieberson 1985: 93).
Még egy dolgot érdemes ezen a ponton megemlíteni. Korábban arról beszéltünk, hogy azokban a kutatásokban, amelyeknek célja egy jelenség elõrejelzése, a nagy R2 általában örvendetes tény, és valóban, a legtöbb tankönyv a sikeres elõrejelzés feltételeként említi a determinációs együttható magas értékét (például Lewis-Beck 1993: 16). Amikor azonban a nagy R2 pusztán annak eredménye, hogy modellünket az éppen megfigyelt adatok esetlegességeihez igazítottuk - vagy, ahogyan sokszor nevezik, tõkét kovácsoltunk a véletlenbõl (Kennedy 1992: 70) -, akkor a nagy R2 egyáltalán nem feltétlenül garantálja, hogy a modell az adott konkrét mintán kívül is ugyanolyan tökéletes lesz. Sõt, Mayer elemzései éppenséggel azt bizonyítják, hogy "amennyiben olyan hipotézisek érdekelnek bennünket, amelyek a minta által felölelt idõszakon túl is érvényesek, akkor az illeszkedés mutatói igen gyenge iránymutatást jelentenek csupán" (Mayer 1975: 882).
Azt, hogy mennyire gyenge lehet ez az iránymutatás, megtudhatjuk
Lieberson (1985: 97-99) találó példájából.
Képzeljük el, hogy nagy számú szabályos
pénzdarabot dobunk fel, mindegyiket egymás után tízszer.
Ha megszámoljuk, a tízbõl hány alkalommal kaptunk
"fej"-et, az eredmény érménként változó
lesz. Lesznek pénzdarabok, amelyek esetében a "fej"-ek száma
csupán kettõ vagy három - az elméletileg várt
öt helyett -, lesznek azonban olyanok is, amelyek esetében
nyolc, kilenc, sõt akár tíz "fej"-et kapunk. Tegyük
föl, hogy megpróbáljuk megmagyarázni ezt az ingadozást;
azt, hogy a "fej"-ek száma egyes érméknél miért
olyan alacsony, másoknál pedig miért olyan magas.
Ha elég kitartóak és türelmesek vagyunk, rábukkanhatunk
a pénzdaraboknak azokra az egyedi vonásaira, amelyek összefüggenek
a "fej"-ek számával. Ilyen vonás lehet például
az, hogy mikor készült az adott érme, hol gyártották,
a számos pénzdarab közül hányadikként
dobtuk fel stb. Bármily szorgalmasak vagyunk is azonban, bármennyi
tulajdonságot veszünk is figyelembe, erõfeszítésünknek
az égvilágon semmi értelme: azok az érmék
ugyanis, amelyek az általunk elvégzett dobássorozatban
nagy számú "fej"-et eredményeztek, és amelyeknek
a tulajdonságait oly lázasan kutattuk, újabb sorozatban
pontosan ugyanakkora valószínûséggel
eredményeznek nagy számú "fej"-et, mint azok a pénzdarabok,
amelyek esetében az elsõ körben a "fej"-ek száma
igen alacsony volt. Míg tehát magyarázó modellünk
kiválóan illeszkedik az adott konkrét dobássorozat
eredményéhez, az érmék tulajdonságainak
szerepét, elõrejelzõ képességét
illetõen teljesen értéktelen. Mindennek alapján
Lieberson joggal vonja le a következtetést, hogy a "megmagyarázandó
variancia" szükséges mértékét alkalmasint
túl is lehet becsülni, és ez a túlbecsülés
kedvezõtlen következményekkel járhat. Egyebek
között arra ösztönzi a kutatót, hogy ad hoc
magyarázatok kitalálásával növelje
az R2 értékét, vagyis olyan eljárásra
csábít, aminek hosszú távon nincs semmi haszna.
Az R2 és a megfigyelések aggregálása
Bizonyára sokaknak feltûnt már, hogy azokban a vizsgálatokban, amelyek régiókat vagy országokat hasonlítanak össze egymással, az R2 értéke rendszerint lényegesen magasabb, mint az egyének megkérdezésén alapuló kérdõíves kutatásokban. Ennyivel okosabbak lennének a területi elemzéseket végzõk, mint azok, akik a survey módszerét választják? Ennyivel jobb, tökéletesebb modelleket tudnának felállítani? A kérdés bonyolult, az azonban egyértelmû, hogy önmagában a magasabb R2 nem bizonyítja ezt. Ez ugyanis alapvetõen nem a kutató képességeinek, hanem az adatok aggregálásának köszönhetõ: amikor az egyénekre vonatkozó megfigyeléseket csoportokba vonjuk össze, és az eredetiek helyett ezekkel a csoportosított adatokkal dolgozunk, az adatpontok általában a korábbinál jobban "rásimulnak" a regressziós egyenesre, növelve ezzel a determinációs együttható értékét. Az aggregálásnak ezt a hatását szemlélteti az alábbi két, hipotetikus adatokon alapuló rajz. Az 1. ábra 5 különbözõ régióban lakó 20 egyén iskolai végzettségének és jövedelmének az adatait tartalmazza; az adatpontok melletti számok a lakóhelyet - a régió sorszámát - jelölik.
1. ábra
Egyénekre vonatkozó adatok
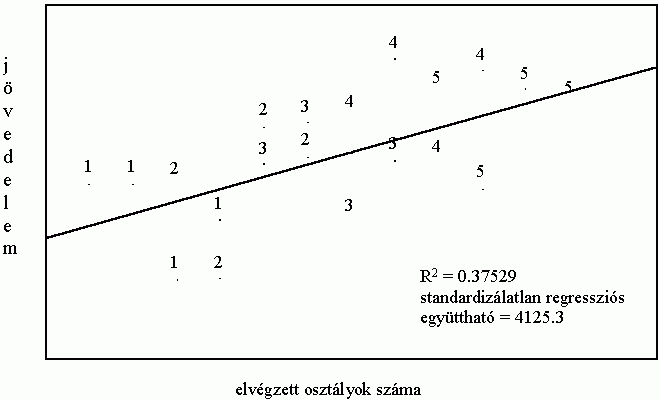
Látható, hogy az ugyanabban a régióban élõk jövedelme különbözik egymástól; az azonos sorszámot viselõ egyénekre vonatkozó adatok szóródnak az adott régió átlaga körül. Ez a szóródás "tûnik el" akkor, amikor az adatokat régiónként aggregáljuk, s az egyéni adatok helyett a régiók átlagait használjuk. Ennek eredménye pedig az a rendkívül szoros illeszkedés, amit a 2. ábra mutat, és amit az R2 magas értéke (0.87) is tükröz. (Érdemes megjegyezni, hogy miközben a determinációs együttható két és félszeresére nõtt, a standardizálatlan regressziós együttható alig változott. Általában elmondható, hogy ez utóbbi mutató kevésbé érzékeny az adatok aggregálására.)9
2. ábra
Aggregált adatok
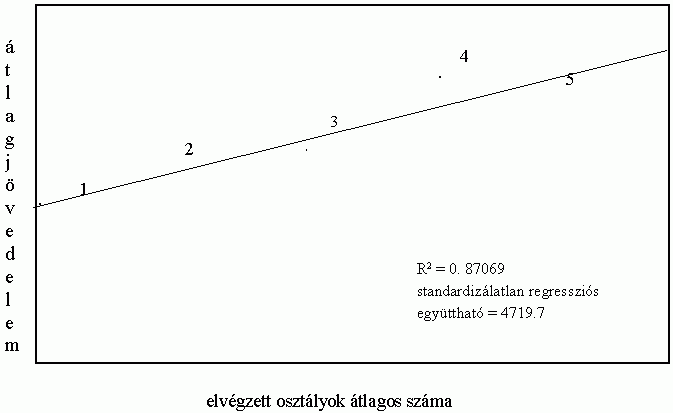
Az aggregálás imént bemutatott hatása mögött
általánosabb összefüggést ismerhetünk
fel. A determinációs együttható értékét
döntõen meghatározza, hogy mekkora azoknak az egyéb
tényezõknek a súlya, szerepe, amelyek szintén
befolyásolják a függõ változót,
ám nem korrelálnak az általunk vizsgált magyarázó
változóval (Darlington 1990: 19). Ha ezeknek az egyéb
tényezõknek - amelyeket a regressziós modell hibatagjában
foglalunk össze, és amelyeket az elemzés során
"zavaró változókként" kezelünk - csökken
a súlya, akkor,- feltéve, hogy minden más változatlan,
az R2 értéke nõ. Az adatok aggregálása
az elõzõ példában éppen ilyen csökkenést
eredményezett: az egyes egyénekre vonatkozó megfigyelések
régiónkénti átlagolásával mintegy
kiszûrtük vagy közömbösítettük a
jövedelmet meghatározó számtalan tényezõ
jelentõs részét (Blalock 1964: 99-101, 112-114).10
Befejezés
Áttekintve a determinációs együtthatóval kapcsolatos különféle értelmezéseket, rávilágítva e mutató fogyatékosságaira, befejezésül hasznos lehet szemügyre venni egy olyan formulát, amely mintegy összefoglaló képet nyújt az R2-et befolyásoló tényezõkrõl, és ezáltal segíthet jobban megérteni e mutató természetét.11 Ehhez elsõ lépésként idézzük fel az (1) egyenlõséget:
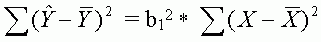
Emlékezzünk, ennek az egyenlõségnek a bal oldala nem egyéb, mint a regressziónak tulajdonítható eltérésnégyzet-összeg, vagyis az R2 számlálója.
Ismeretes, hogy a teljes eltérésnégyzet-összeg - tehát az R2 nevezõje - két részbõl, a regressziónak tulajdonítható és a maradék vagy reziduális négyzetösszegbõl áll:
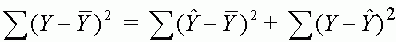 2
2
Helyettesítsük most be a (2) egyenlõségbe az (1) egyenlõséget:
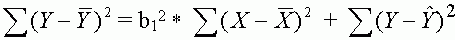
Mindezek alapján a determinációs együtthatót a következõképpen írhatjuk fel:
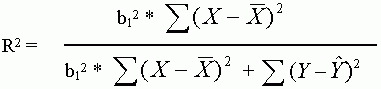
Szavakkal ezt így fogalmazhatjuk meg:
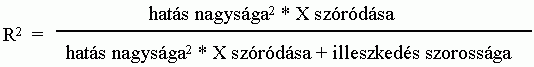
Ebbõl jól látható, hogy a determinációs
együtthatóban háromféle tényezõ
keveredik: a magyarázó változó hatása,
ennek a változónak a szóródása, és
végül a regressziós modell illeszkedésének
a "jósága" vagy szorossága. Éppen mert egyszerre
ennyi különbözõ tényezõtõl függ,
az R2 ezek egyikének mérésére sem
igazán alkalmas. Sem a magyarázó változó
hatását, annak nagyságát nem tükrözi
pontosan, sem pedig a regressziós modell illeszkedését.
Mindkét feladatra jobb mutatók állnak rendelkezésünkre:
a hatás nagyságának mérésére
a standardizálatlan regressziós együttható, az
illeszkedésére pedig a becslés standard hibája.
Mindezek fényében az a tisztelet, ami a determinációs
együtthatót rendszerint övezi, nem tûnik megalapozottnak;
népszerûségét ez a mutató alighanem inkább
retorikai értékének, mintsem tényleges teljesítményének
köszönheti.
Jegyzetek
* A cikk egy korábbi változatához
fûzött megjegyzéseiért köszönettel tartozom
Hegedûs Ritának, Lengyel Györgynek és Róna-Tas
Ákosnak.
1. A szakirodalom gyakran különbséget
tesz r2 és R2, "egyszerû" és
többszörös determinációs együttható
között. Mivel mondanivalóm egyformán vonatkozik
mindkét mutatóra, fölöslegesnek ítéltem
e megkülönböztetés hangsúlyozását,
és az "R2", illetve a "determinációs együttható"
kifejezéseket felváltva, azonos értelemben használtam.
Ez a némi pongyolaság - úgy gondolom - nem okoz majd
félreértést, viszont gördülékenyebbé
teszi a szöveget.
2. Az elõrejelzés problémakörén
belül speciális esetnek tekinthetõ az a bizonyos fokig
módszertani jellegû feladat, amikor egy változó
valamilyen okból hiányzó értékeit igyekszünk
pótolni más változóknak és az e változók
hatását kifejezõ regressziós együtthatóknak
a felhasználásával. A regresszióelemzésnek
erre a fajta alkalmazására példa a foglalkozások
presztízspontszámának meghatározása
a foglalkozások egyéb jellemzõi alapján (Loether-McTavish
1980: 362-363), de az ún. kisterületi becslésnél
is találkozunk ezzel a megközelítéssel (Marton
1985: 68-69; Ericksen 1973).
3. Ezt még azok a szerzõk is elismerik,
akik egyébként védelmükbe veszik a determinációs
együtthatót. Lewis-Beck és Skalaban például
így fogalmaz: "amikor a kutató X [változó]
hatására kíváncsi, az R2 -nek kevés
haszna van. Ebben az esetben a figyelmet a megfelelõ regressziós
együtthatóra és annak standard hibájára
kell fordítani" (Lewis-Beck-Skalaban 1991: 169).
4.Az egyenlõség bizonyításához
elõször is írjuk föl a regressziós egyenletet:
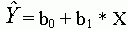
ahol 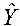 a függõ változó
becsült értéke, X a magyarázó változó,
b0 és b1 pedig a regressziós együtthatók.
Mivel
a függõ változó
becsült értéke, X a magyarázó változó,
b0 és b1 pedig a regressziós együtthatók.
Mivel
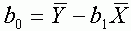
ahol 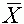 és
és  a
magyarázó, illetve a függõ változó
átlaga, ezért
a
magyarázó, illetve a függõ változó
átlaga, ezért
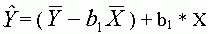
Emeljük ki a b1 együtthatót, Y átlagát
pedig vigyük át a bal oldalra:
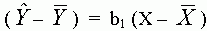
Végül emeljük négyzetre és összegezzük
minden megfigyelésre az egyenlõség mindkét
oldalát:
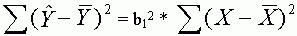
5. Egy dichotóm változó varianciája
ugyanis nem más, mint a két kategória relatív
gyakoriságának a szorzata; ez a szorzat pedig akkor maximális,
ha az összeszorzandó relatív gyakoriságok azonosak.
6. Ennek feltétele azonban a homoszkedaszticitás,
vagyis az, hogy a hiba szórása a magyarázó
változó minden értéke esetében azonos
legyen.
7. Mindazonáltal, ha a becslési hibának
közvetlen gyakorlati jelentõsége van, akkor a regressziós
becslés standard hibája nem szükségképpen
a legjobb választás. Ez a mutató ugyanis a megfigyelt
és a becsült értékek közötti eltérések
négyzetén alapul, és ily módon nagyobb súlyt
ad a nagyobb, és kisebb súlyt ad a kisebb eltéréseknek.
Elképzelhetõ azonban, hogy a becslési hibák
gyakorlati következményei - például a velük
járó költségek - szempontjából
minden hiba egyformán lényeges; ha ez a helyzet, akkor az
eltérések négyzete helyett indokoltabb lehet azok
abszolút értékét használni. (A négyzetes
és az abszolút hibák közötti választás
kérdésérõl bõvebben lásd Berk
1986; az elõrejelzési hibák költségeinek
figyelembevételérõl általában pedig
lásd Goodman 1966.)
8. Más kérdés, hogy a program
hatását kifejezõ regressziós együttható
standard hibájának csökkentése érdekében
a randomizálás ellenére is hasznos lehet e kontrollváltozók
szerepeltetése, ez ugyanis mérsékli a reziduális
szórást, ezen keresztül pedig a standard hibát.
9. Ez azonban nem jelenti azt, hogy az aggregálás
sohasem befolyásolja a standardizálatlan regressziós
együttható értékét. Amennyiben az adatok
csoportosítása nyomán specifikációs
hiba jön létre, ez a mutató is torzul. Az aggregálásnak
a különféle statisztikai mutatókra gyakorolt hatásáról
bõvebben lásd például Blalock 1964; Langbein-Lichtman
1978; Hanushek et al. 1974.
10. Egy másik módja annak, hogy a "zavaró
változók" szerepét mérsékeljük,
s ezáltal a vizsgált magyarázó változó
relatív súlyát, fontosságát növeljük,
a függõ változó pontosabb mérése.
11. Az alábbi levezetéshez az ötletet
Christopher Achen (1982: 63) tanulmánya adta.
Hivatkozások
Achen, Ch. 1982. Interpreting and Using Regression. Beverly Hills-London: Sage Publications
Berk, R. A. 1986. How Aapplied Sociology Can Ssave Basic Sociology. Unpublished manuscript.
Blalock, H. 1964. Causal Inferences in Nonexperimental Research. Durham, N. C.: University of North Carolina Press
Cook, Th.-D. T. Campbell 1979. Quasi-Experimentation. Design and Analysis Issues for Field Settings. Boston etc.: Houghton Mifflin Co.
Cramer, J. S. 1987. Mean and Variance of R2 in Small and Moderate Samples. Journal of Econometrics, 35, 253-266.
Darlington, R. 1990. Regression and Linear Models. New York etc.: McGraw-Hill Publishing Co.
Elster, J. 1997. A társadalom fogaskerekei. Osiris Kiadó
Ericksen, E. P. 1973. A Method for Combining Sample Survey Data and Symptomatic Indicators to Obtain Estimates for Local Areas. Demography, 10, 137-160.
Ezekiel, M.-K- Fox 1970. Korreláció- és regresszió-analízis. Lineáris és nem-lineáris módszerek. Budapest: Közgazdasági és Jogi Könyvkiadó
Glenn, N. D.-B. A. Shelton 1983. Pre-Adult Background Variables and Divorce: a Note of Caution about Overreliance on Explained Variance. Journal of Marriage and the Family, 45: 405-410.
Goodman, L. 1966. Generalizing the Problem of Prediction. In: P. F. Lazarsfeld-M. Rosenberg (eds.) The Language of Social Research. 5th ed., Toronto, 277-281.
Hanushek, E. A. et al. 1974. Model Specification, Use of Aggregate Data, and the Ecological Correlation Fallacy. Political Methodology, 1, 89-107.
Kennedy, P. 1992. A Guide to Econometrics. Oxford, UK.-Cambridge, USA Blackwell Publishers
King, G. 1986. How Not to Lie with Statistics: Avoiding Common Mistakes in Quantitative Political Science. American Journal of Political Science, 30, 666-687.
- 1991. "Truth" is Stranger than Prediction, more Questionable than Causal Inference. American Journal of Political Science, 35, 1047-1053.
Langbein, L. I.-A. J. Lichtman 1978. Ecological Inference. Beverly Hills-London: Sage Publications
Lewis-Beck, M. 1978. Stepwise Regression: a Caution. Political Methodology, 5, 213-240.
- 1993. Applied Regression: an Introduction. In: M. Lewis-Beck (ed.) Regression Analysis. International Handbooks of Quantitative Applications in the Social Sciences,. 2. London-Thousand Oaks, CA-New Delhi: Sage Publications
Lewis-Beck, M.-A. Skalaban 1991. The R-Squared: Some Straight Talk. Political Analysis, 2, 153-171.
Lieberson, S. 1985. Making it Count. The Improvement of Social Research and Theory. Berkeley-Los Angeles-London: University of California Press
Loether, H. J.-D. G. McTavish 1980. Descriptive and Inferential Statistics: an Introduction. Boston etc.: Allyn and Bacon, Inc.
Marton Á. (szerk). 1985. Területi és egyéb szempontok szerint részletezett statisztikai mutatószámok becslése. Budapest: Központi Statisztikai Hivatal
Mayer, T. 1975. Selecting Economic Hypothesis by Goodness of Fit. Economic Journal, 85, 877-883.
Pedhazur, E. 1982. Multiple Regression in Behavioral Research. 2nd ed. Forth Worth etc.: Harcourt Brace Jovanovich College Publishers
Weisberg, S. 1985. Applied Linear Regression. 2nd ed. New York
etc.: John Wiley & Sons