Formalizálási stílusok, elméleti következmények

Egy új elméletépítési módszer, logikai formalizálás alkalmazását mutatja be az írás a szervezetökológia inerciatételét elemezve. Milyen körülmények mellett igaz, hogy a szervezeti átalakulást fékezõ tehetetlenség - az inercia - túlélési elõny? Szemügyre vesszük az elmélet egy korábbi logikai formalizálását, mely szerintünk szükségtelenül korlátozó premisszákból vezeti le az inerciatételt. Ezután két új, az eredeti érvelést szorosan követõ logikai formalizálást adunk az inerciaelméletre, amelyek sokat megõriznek a természetes nyelvi elmélet tágasságából. Miért jobb kétszer, mint egyszer? A két formalizálás az érvelés más-más oldalait emeli ki. Így nem meglepõ, hogy a két logikai modell más-más kapukat nyit a tágabb elmélet, a szervezetökológia többi részéhez. A tanulmány végén a két formalizálásból adódó fogalmi elágazásokat mutatjuk be, szemléltetve a logikai formalizálás elméletépítési aktusát.
 

A szervezetelmélet tanulmányozása folyhat tudományos érdeklõdésbõl, de gyakorlati megfontolásból is: a beruházók, vállalkozók tudni akarják, melyek a feltételei annak, hogy sikeres szervezeteket hozzanak létre. A siker mércéje lehet például a profit, a tõzsdei érték, a tõke forgási sebessége, a növekvõ piaci részesedés. Kellõen nagy minta esetén vizsgálható, hogy milyen szerkezeti elemek, stratégiák, a tevékenységi kör milyen megválasztása vezet sikerhez a piaci környezet különbözõ állapotaiban. Problémát okoz azonban, hogy a sikert mérõ tulajdonságok nem függetlenek egymástól, és hogy a korreláció közöttük nem is mindig pozitív, továbbá hogy a szervezetek hajlandóságot mutatnak a siker színlelésére. Sokszor könyvelõi döntés függvénye, hogy egy adott sikerismérvet tekintve, a szervezet sikeres-e. Van azonban egy olyan szervezeti tulajdonság, amely az ügyes könyvelõk által is csak nehezen színlelhetõ, és amely így a szervezeti siker egyik (korlátozott alkalmazhatóságú) mércéje lehet: nevezetesen az, hogy életben marad-e az adott szervezet. Ha igen, akkor nem lehet teljesen sikertelen. Nem elég azonban a vizsgálatokat a sikeres szervezetek tanulmányozására korlátozni, mert ez nem teszi lehetõvé a sikerrel véletlenszerûen együtt járó és a sikerért felelõs tulajdonságok elkülönítését. Ezért érdemes megvizsgálni a hasonló jellegû, egymással versenyzõ szervezetek együtteseit, a szervezetek populációt is. Ilyen megfontolások vezettek a szervezetökológia megalapítására.

A szervezetökológia két évtizedes története M. T. Hannan és J. Freeman programadó cikkével kezdõdött (Hannan-Freeman 1977). A kutatási terv röviden így fogalmazható meg: a szervezeti népesedési folyamatok (születés és halandóság) tanulmányozása különbözõ szervezeti tulajdonságok függvényében. Az 1977-es írás megjelenését követõ empirikus vizsgálatokból leszûrt elméleti eredményeket egy évtizeddel késõbb az Organizational Ecology címû könyvükben foglalták össze a szerzõk (Hannan-Freeman 1989). Azóta a szervezetökológia a szervezetszociológia egyik legerõteljesebben kutatott ágává lett, a nagyobb amerikai (s kisebb részt európai) szociológiai folyóiratokban lapozva, empirikus vizsgálatokról beszámoló írások sokaságát találjuk. Néhány ismert példa: amerikai, dán, koreai és japán bankok, amerikai és bolgár napilapok, olasz internetújságok, kaliforniai vendéglõk, sörfõzdék és borgazdaságok, amerikai és európai autógyárak, amerikai szakszervezetek, telefontársaságok és bicikligyárak. Ezek az empirikus vizsgálatok a sikert (életben maradást) befolyásoló tulajdonságok széles körét vették figyelembe: életkor, méret, a szervezet életterének - a szervezeti niche - szélessége, a felbukkanó új lehetõségek megragadásának sebessége, a technikai újdonságok felhasználási sebessége stb. Ezekrõl a fejleményekrôl és a vonatkozó irodalomról Carroll-nak és Hannan-nek a szervezetökológia helyzetét összefoglaló könyvében olvashatunk (1999).

Az idõközben felhalmozódott empirikus tudás a korábbi, néha csak vázlatosan körvonalazott elméleti elgondolások pontosítását, esetenként módosítását tette szükségessé. Megfogalmazódott az igény, hogy a szervezetökológia elméletét érdemes az alapoktól újragondolni, és hogy ez a további elméletépítést elõsegítõ, áttetszõ szerkezetet adó, formális következtetések levonását lehetõvé tevõ logikai formalizálás alkalmazásával történjék. Ennek a munkának egyik szeletét adjuk most közre, amely a szervezetökológia tehetetlenség vagy inerciaelméletét elemzi a formális logika eszközeivel, a szociológiai tartalom pontosabb kifejtése érdekében.¹

Az inerciaelmélet kitüntetett helyet foglal el a szervezetökológián belül. Mint írtuk, a szervezetökológia a társadalmi kiválasztódási folyamatoknak a szervezetpopulációkra gyakorolt hatását vizsgálja. Egy populáció összetétele kétféleképpen módosulhat. Változhat úgy, hogy a populációt alkotó szervezetek jellemzõi változnak meg, például mert a szervezetek alkalmazkodnak a környezetükhöz. De módosulhat a populáció úgy is, hogy nem a tagjai változtatják meg a tulajdonságaikat, hanem a környezeti hatásokhoz nem illeszkedõ szervezetek kihullanak, és helyüket újak foglalják el. Az újonnan jött szervezetek közül a környezethez jól illeszkedõk a többieknél jobb eséllyel maradnak meg a színen. A társadalmi kiválasztódási folyamatok mûködése nem feltételezi a szervezetek alkalmazkodó képességének (adaptation) a meglétét. A kiválasztódás mûködhet úgy is, hogy új szervezetek veszik át a régiek helyét. A kiválasztódási folyamat akkor is végbemegy, ha az újonnan alapított szervezetek teljesen véletlenszerû tulajdonság-összetétellel lépnek a színre. Ilyen esetekben nem az egyes szervezetek "alkalmazkodnak" a körülményekhez tulajdonságaik megváltoztatásával, hanem maga a populáció, alkalmatlan tagjainak elhullatásával. Az egyed tulajdonságainak változásával végbemenõ kiválasztódást lamarckinak, az alkalmatlanoknak a új egyedekkel való felváltásával végbemenõ kiválasztódást darwininak nevezik a biológiában. A közgazdaságtan és a vezetéstudomány szemlélete alapvetõen a lamarcki - a szervezetek alkalmazkodási képességének szerepét hangsúlyozza. Ezzel szemben a szervezetökológia a darwini mintát követi a kirostálódáson és újranépesülésen alapuló populációszintû alkalmazkodást helyezve az elemzés középpontjába (Hannan-Freeman 1989).²

A fentiekbõl következik a szervezeti tehetetlenségnek a szervezetökológia kutatási módszertanában betöltött fontos szerepe. Az inerciaelmélet központi állítása, a késõbbiekben részletesen elemzett inerciatétel azt mondja ki, hogy a változásra képtelen, nagy tehetetlenségû szervezetek bizonyos körülmények között elõnyt élveznek a kiválasztódás során. Viszont ha igaz az, hogy a szerkezetüket megváltoztatni képes, kis inerciájú szervezetek gyorsan kipenderülnek a színrõl, úgy a szervezetpopulációk összetételének két fent említett változási módja közül elegendõ csak az egyiket vizsgálni. Azt, amelyiknél az alkalmatlan szervezetek forgalomból való kivonásával s újakkal való pótlásával alakul a populáció összetétele. Ennek megfelelõen a szervezetökológia empirikus vizsgálatainak a középpontjában a szervezetek népesedési (születési és halálozási) folyamatainak megfigyelése áll. Hangsúlyoznánk azonban, hogy a fenti módszertani megfontolás alkalmazhatóságának van egy további, ebben az írásban nem vizsgált feltétele: a kis tehetetlenségû szervezetek kiszóródásának hevenynek, gyors lefolyásúnak kell lennie a populáció összetételét alakító többi népesedési folyamatéhoz képest.

Bár ebben a tanulmányban az elméleti elemzésre helyezzük a hangsúlyt, megemlítjük, hogy az empirikus kutatás feltárta a szervezeti inercia elterjedésének közvetlenül megfigyelhetõ következményeit is. Megállapították például, hogy a munkavállalói jogok alapításkori állapota mintegy belefagy a szervezetekbe, s még évtizedekkel késõbb is megfigyelhetõ eltéréseket okoz az egy idõs szervezetek részpopulációiban (Hannan-Burton-Barron 1996; Barron-Burton-Hannan 1996). Kiemelnénk, hogy a mai magyarországi állapotok kiváló terepet nyújtanak e jelenség tanulmányozására.

A következõkben amellett érvelünk, hogy a szervezeti tehetetlenség elméletének igaza van, elõször természetes nyelven, késõbb logikai formulák segítségével. Elõször ismertetjük az inerciaelméletet, majd az inerciatétel egy korábbi logikai formalizálását vizsgáljuk, rámutatva annak - az elmélet érvényességet szükségtelenül leszûkítõ - hiányosságaira. Ezt követõen lényegesen gyengébb szociológiai megszorításokra jutó feltevésekbõl vezetjük le az inerciatételt. Végül a két új logikai modellnek a szervezetökológia más ágaihoz való kapcsolódási lehetõségét vizsgáljuk, a zárófejezet pedig összefoglalja, hogy mire jutottunk.
 

2. Az inerciatétel természetes nyelvi megfogalmazása

A szervezeti tehetetlenség - az inercia - a környezeti hatásokhoz való alkalmazkodás hiányában vagy késedelmes voltában mutatkozik meg. A szervezeti tehetetlenség fogalma valamelyest párhuzamba állítható a fizika inercia fogalmával. Newton elsõ törvénye szerint a békén hagyott testek nem változtatnak mozgásállapotukon. Sebességük megváltoztatásához külsõ hatásra, erõre van szükség, melynek mértékét a test tehetetlen tömege és a megcélzott változás nagysága szabja meg. Hasonlóan, a környezeti adaptációs nyomásnak való ellenszegülés mértéke a szervezeti tehetetlenség. Az alkalmazkodási képességet központba helyezõ gondolkodás nézõpontjából az inerciatétel idegenül hangzik: hektikusan változó gazdasági-társadalmi körülmények közepette a kiválasztódás rostáján inkább a magas tehetetlenségû szervezetek maradnak fenn (Hannan-Freeman 1977; 1984; 1989).

Az állítás szokatlansága eltûnik azonban, ha figyelembe vesszük a szervezeti tehetetlenség egy másik, jótékony és elõnyt hordozó tulajdonságra akaszkodó potyautasként halmozódik fel a túlélõ szervezetekben, a társadalmi kiválasztódási folyamatok szándékolatlan melléktermékeként (Hannan-Freeman 1984; 1989). Ez a következõképpen történhet. A szervezetek jelentõs részben felelõs voltuk (accountability) és megbízhatóságuk (reliability) miatt válhattak korunk mindenütt jelen lévõ társadalmi szereplõivé.³ A felelõs jelzõt itt abban az értelmében használjuk, ahogy például felelõs kormányról beszélünk, amely cselekedeteiért a parlamentnek tételes számadással tartozik. Valamely szervezet felelõs volta a vizsgált elméleti környezetben annyit jelent, hogy a szervezet képes racionálisan számot adni a tevékenységérõl. A racionalitás normái által áthatott világunkban erõs a nyomás, hogy a társadalmi szereplõk döntéseiket eszköz-cél fogalmakban fejtsék ki.

A szervezeti megbízhatóság az elmélet környezetében azt jelenti, hogy a szervezet képes szûk tûréshatárok között tartani tevékenysége minõségének és idõzítésének ingadozásait. A jövendõ bizonytalan. A befektetõk, partnerek és leendõ szervezeti tagok a megbízhatóságot és kiszámíthatóságot a hatékonyságnál is magasabbra értékelhetik. A partnerek szeretik, ha a keresett termék vagy szolgáltatás bizonyosan elérhetõ, amikor csak szükség van rá, méghozzá az ismert színvonalon.

A nagy megbízhatóságú és felelõs szervezeteknek azonban a tehetetlenségük is nagy. Mindkét jótékony vonás megléte egy harmadik jellemzõnek, a szerkezet önfenntartó képességének (reproducibility) a függvénye. Az önfenntartó képesség megléte arra utal, hogy a szervezet képes szerkezetét napról napra pontosan újjáépíteni. Ez bejáratott szervezeti rutinok létét feltételezi (Nelson-Winter 1982). Emiatt a szerkezetük, mûködésük önfenntartására képes szervezetek egyúttal ellenállóak az átalakítási kísérletekkel szemben. Ennek az ellenállásnak a mértéke a szerkezeti tehetetlenség. A magas önfenntartó képességû szervezeteket holt teher jellemzi: a környezeti változásokra adott válasz jóval a kiváltó hatás után kullog. A késedelem gyakran hosszabb, mint maga a választ kiváltó környezeti ingadozás. Ilyenkor a szervezeti tehetetlenség teljesen leblokkolhatja a változásra tett kísérleteket.

A fenti szempontokat a következõ feltevés-következtetés formában foglalta össze Hannan-Freeman (1984):

2. 1. feltevés. A kiválasztódás a felelõs és megbízható formáknak kedvez a modern társadalmak szervezetpopulációiban.
2. 2. feltevés. Valaminek a felelõs és megbízható volta nagyfokú szerkezeti önfenntartó képességet követel.
2. 3. feltevés. A szerkezet önfenntartó képessége tehetetlenséget hoz létre.
2. 1. tétel. A kiválasztódás a nagy szerkezeti tehetetlenséggel rendelkezõ szervezeteknek kedvez a modern társadalmak szervezetpopulációiban.⁴

Hannan-Freeman (1984) szerint a három feltevésbõl (2. 1-2. 3. feltevés) következik az inercia 2. 1. tételbeli megfogalmazása. A fenti érvelés helyes voltát az írás megjelenését követõen sokszor megkérdõjelezték. A természetes nyelven elmondott érvelések következtetési szerkezete nem mindig áttetszõ. A vitát eldöntendõ került sor az inerciaelmélet logikai vizsgálatára. Hannan és Freeman érvelésének racionális rekonstrukcióját és logikai formalizálását Péli-Bruggeman-Masuch-Ó Nualláin (1994) végezte el, amelyet röviden a következõkben ismertetünk (munkájukra a továbbiakban az 1994-es formalizálásként hivatkozunk.)
 

3. Inerciatétel, racionális rekonstrukció

Cikkünk elsõrendû állításlogikát (first-order predicate logic, FOL) használ.⁵ Az 1994-es formalizálás vizsgálat alá vett része a FOL egy technikailag egyszerû részére, az úgynevezett propozicionális logikára épül, amelyben nem szerepelnek változók és logikai kvantorok ("létezik", "minden").

Az elsõ fontos döntés az elemzés szintjének tisztázása volt: szervezetek populációiról vagy egyedi szervezetekrõl beszélünk. A 2. 1. feltevés és a 2. 1. tétel szervezetek populációit említi. Ezzel szemben 2. 2. és 2. 3. feltevés inkább egyedi szervezetekrõl szólnak. De mind a négy kijelentés értelmezhetõ úgy, hogy egy tetszõlegesen kiválasztott egyedi szervezetrõl szól. Az 1994-es formalizálást egy némileg egyszerûbb, egyúttal magyarra fordított jelölésrendszerbe átírva mutatjuk be. A változtatás nem érinti az érvelést. Jelöljék az önfenntartó, felelõs, megbízható és tehetetlen predikátumok rendre, hogy a vizsgált szervezet rendelkezik a szóban forgó tulajdonságokkal. Jelölje a kedvezményezett predikátum azt a tényt, hogy a szervezet a kiválasztódás kedvezményezettje (selection favored).

3. 1. feltevés. Ha egy szervezet felelõs és megbízható, akkor a kiválasztódás kedvezményezettje:

A 2. 2. feltevés formalizálásakor el kellett dönteni, mit jelent a "megkövetel" (requires) ige ebben az elméleti környezetben. Az "A megköveteli B-t" kifejezés a logikai értelemben vett szükséges feltételre utal .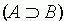

3. 2. feltevés. Ha egy szervezet felelõs és megbízható, akkor a szerkezete önfenntartó:

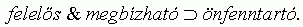
A 2. 3. feltevésben a "létrehoz" (generates) ige szerepel. Az "A létrehozza B-t" kifejezés oksági viszonyra utal, és 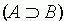 formában fordíttatott. Kiemelnénk, hogy az okság összetett fogalma általánosságban nem egyszerûsíthetõ egy logikai implikációra. Számunkra azonban a modellben a "létrehozatal" végeredménye fontos: ha az ok fennáll, akkor az okozat is megjelenik.

3. 3. feltevés. Ha egy szervezet szerkezete nagy önfenntartó képességû, akkor egyúttal nagy tehetetlenségû:

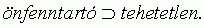
Végül az inerciatétel így lett formalizálva:

3. 1. tétel. Ha egy szervezet nagy szerkezeti tehetetlenségû, akkor a kiválasztódás kedvezményezettje:

Fájdalom, a 3. 1. tétel nem következik a 3. 1-3. 3. feltevésbõl.
 

4. Inerciatétel, módosított formalizálás (1994)

Az 1994-es formalizálás következõ lépéseként a szerzõk gyógyírt kerestek a problémára. Kérdés, hogy milyen módosításokkal válik levezethetôvé az inerciatétel, s e változtatásoknak mi a szociológiai ára. A javaslat így szólt: fordítsuk meg a következtetés irányát a 3. 2. és 3. 3. feltevésekben, s a 3. 1 tétel jelöltbõl valódi tétellé válik. De mivel az elõzõ pontban ismertetett szemantikai elemzést nem kívánták a szerzõk visszavonni (azokat mi is helytállóknak véljük), ezért kettõs implikációt (º ) javasoltak a két kérdéses formulában. Így azok "akkor és csak akkor" jellegû kijelentésekké váltak. A könnyebb követhetõség kedvéért megismételjük a változatlanul hagyott formulákat is:

4. 1. feltevés (egykori 3. 1. feltevés). Ha egy szervezet felelõs és megbízható, akkor a kiválasztódás kedvezményezettje:

4. 2. feltevés. Egy szervezet akkor és csak akkor felelõs és megbízható, ha a szerkezete önfenntartó:

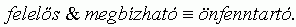
4. 3. feltevés. Egy szervezet akkor és csak akkor önfenntartó szerkezetû, ha nagy szerkezeti tehetetlenségû:

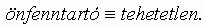
4. 1. tétel. Ha egy szervezet nagy szerkezeti tehetetlenségû, akkor a kiválasztódás kedvezményezettje:

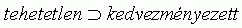
A tétel így már következik a feltevésekbõl, de örömünk nem felhõtlen: az elmélet érvényességi körének tetemes szûkítése az ár, amit fizetni kellett. A 4. 2.-4. 3. feltevések két további megszorító feltevést tartalmaznak a 3. 2.-3. 3. feltevésekhez képest.

A 4. 2. feltevések aszerint nem lehetséges olyan szervezet, amelyik rendelkezik a szerkezeti önfenntartó képesség adományával, ám ezzel együtt sem képes megbízható és felelõs mûködésre. Tudjuk azonban, hogy vannak ilyen balek szervezetek. Hajlunk azt mondani, hogy az önfenntartó képesség csupán lehetõséget, nem pedig biztosítékot nyújt e két szervezeti erény eléréséhez. De megeshetik az is, hogy az olajozottan mûködõ szervezeti rutinok, az önfenntartó képesség hordozói elavulnak, ahogy a környezet fokozatosan "elmozdul" egy másik állapot felé. Az agonizáló rutinok ilyenkor túlélhetik a kiszámítható (megbízható és felelõs) szervezeti mûködést. A 4. 2. feltevéssel megterhelt inerciaelmélet ezekre a helyzetekre mind-mind nem vonatkozhat.

A 4. 3. feltevés a korábbi változattal (3. 3. feltevés) szemben olyan helyzetekre korlátozódik, ahol a nagy tehetetlenségû szervezetek kivétel nélkül magas szerkezeti önfenntartó képességûek. Azonban számos kialakuló szervezet megreked az "adhocrácia" szintjén (Mintzberg 1979), és nem épít ki nap mint nap újjáépülõ szerkezetet. E szervezetek egy része képtelen vagy egyszerûen csak rest változtatni a szerkezetén, azaz nagy tehetetlenségû. Ez az egyáltalán nem elhanyagolható számban jelen lévõ típus ugyancsak kívül marad a megszorított modell érvényességi körén.⁶

Ezek a hátulütõk arra késztetnek, hogy "olcsóbb", a szociológiai elméletet kevésbé megszorító formális megoldások után nézzünk. Vajon az elmélet ilyen korlátos, vagy csak a formalizálás nem megfelelõ? A következõkben az inerciaérvelés két olyan formalizálását mutatjuk be, amelyek szorosan az elmélet természetes nyelvi érvelése mentén haladnak, de mentesek az említett megszorításoktól. A két formalizálás különbözik mind az elméleti megfontolások, mind az alkalmazott szintaktikai megoldások tekintetében. Késõbb bemutatjuk, hogy a két formális modell más-más kapcsolódást tesz lehetõvé a szervezetökológia más részeihez. A semlegesnek tûnõ technikai megoldások mögött különféle elméleti tartalmak rejlenek, amelyek a további formális elméletépítés során felszínre bukkannak. A formalizálás során technikai köntösben elméleti döntéseket hozunk, amelyek különféle pályákat jelölnek ki az elmélet számára.
 

5. Elsõ újrafogalmazás - a szervezetek mentén

Az 1994-es formalizálás hibái részben abból erednek, hogy a szerzõk kizárólag Hannan és Freeman pontokba szedett kijelentéseire támaszkodtak (2. 1.-2. 3. feltevések), figyelmen kívül hagyva a tágabb elméleti környezetet. A szóban forgó írásban (Hannan-Freeman 1984) benne rejlik az is, ami e három kimondott feltevésbõl hiányzik: nem feltétlenül a szervezeti tehetetlenség jelenléte adja a kiválasztódási elõnyt. Az inercia egy kívánatos vonás, a szerkezeti önfenntartó képességnek kéretlen mellékterméke, akár a rózsán a tüske. A tehetetlenség azáltal erõsödhet fel a szervezetpopulációkban, hogy a túlélõk - megmaradásukat szolgáló erényeik mellett - egyúttal szerkezeti tehetetlenséggel is meg vannak verve. Az érett szervezetpopulációkban az inerciafelhalmozódás a kiválasztódási folyamat következménye: "A megbízhatóságon és felelõsségen alapuló szervezeti mûködés elõfeltétele a szerkezet önfenntartó képessége. A szerkezeti önfenntartó képesség ára szerkezeti tehetetlenség formájában fizettetik meg." (Hannan-Freeman 1984: 162.)

Akárcsak az elõzõekben írottak, a következõ formulák is a populáció egy tetszõlegesen választott szervezetére vonatkoznak. Megítélésünk szerint az 1994-es formalizálás (3. pont) helyesen rekonstruálta Hannan és Freeman második és harmadik (2. 2. és 2. 3.) feltevését, és rossz útra tévedt, amikor ezeket megváltoztatta (4. 2. és 4. 3. feltevés). Ezért elvetjük a bajkeverõ kettõs következtetési nyilakat ("akkor és csak akkor"). Viszont az elsõ feltevésnek és magának az inerciatételnek a megformálása alapvetõ fogalmi változtatásra szorul (4. 1. feltevés és 4. 1. tétel):

5. 1. feltevés. Ha egy szervezet a kiválasztódás kedvezményezettje, akkor megbízható és felelõs:

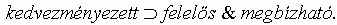
Az átírt feltevés az elõzõ változattal ellentétben nem állítja, hogy a megbízható és felelõs szervezeti mûködés önmagában elegendõ a túléléshez. Megengedi, hogy a kiválasztódást más tulajdonságok is befolyásolják. Az 5.1. feltevés annyit köt ki, hogy a túlélõknek megbízható és felelõs mûködésûeknek kell lenniük. Ez az átfogalmazás összhangban van Hannan és Freeman egy máshol megfogalmazott kiválasztódásértelmezésével: "A szervezeti változatokra és változásokra adott kiválasztódás elemzés (...) sokakat zavarba ejt, mert a feje tetejére állítja az oksági elemzés megszokott logikáját. Az oksági elemzés a szervezetek szintjén azt vizsgálja, hogy miként befolyásolja egy adott tulajdonság megléte más tulajdonságok elõfordulási valószínûségét. Ezzel szemben a kiválasztódás elemzése azt tárja fel, hogy e jellemzõk elõfordulásai (együttes eloszlásaik) hogyan kötõdnek a születési és halálozási arányokhoz, az egyesülési folyamatokhoz és a szervezetek formaváltásaihoz." (Hannan-Freeman 1986: 52-53.)

A jogaiba visszaállított két állítást (3. 2. és 3. 3. feltevést) újból kimondjuk.

5. 2. feltevés (leporolt 3. 2. feltevés). Ha egy szervezet felelõs és megbízható, akkor a szerkezete önfenntartó:

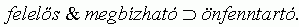
5. 3. feltevés (leporolt 3. 3. feltevés). Ha egy szervezet szerkezete nagy önfenntartó képességû, akkor egyúttal nagy tehetetlenségû:

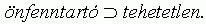
Az inerciatételt 5. 1. feltevéshez hasonló formában mondjuk ki: a kiválasztott szervezetek nagy tehetetlenségûek:

5. 1 tétel. Ha egy szervezet a kiválasztódás kedvezményezettje, akkor nagy tehetetlenségû:

Az 5. 1. tétel az 5. 1., 5. 2. és 5. 3. feltevések logikai következménye.⁷ Kiemelnénk, hogy a tétel ebben a formájában nem állítja, hogy a szervezeti tehetetlenség elegendõ a túléléshez. A nagy inerciájú szervezetek is elhullhatnak. De mindazokban a helyzetekben, mikor az 5. 1., 5. 2. és 5. 3. feltevés fennáll, a túlélõ szervezetek (ha akadnak) bizonyítottan nagy tehetetlenségûek.

Az 1. ábrán egy négy bemenetû Venn-diagram szemlélteti a tétel bizonyítását. A csíkozott területeknek üreseknek kell lenniük: legalább egy feltevés kizárja az adott zóna által jelölt tulajdonságkombinációt. Például a bal felsõ négyzetben csak megbízható és felelõs, de nem önfenntartó szerkezetû szervezetek kerülhetnek; ezek létezését a második feltevés kizárja. Ha egy zóna nem üres, akkor ezt egy beleírt fekete golyó jelöli (erre majd a 2. ábrán látunk példát). A csíkozatlan (nem tiltott) zónákban fordulhat elõ szervezet. De ezek a zónák is üresek maradhatnak, mert a tulajdonságok megengedett kombinációi sem feltétlenül valósulnak meg. Az 1. ábrán ez a helyzet: a három feltevés "ha, ... akkor" szerkezetû, így nem garantálják, hogy az adott tulajdonságokkal jellemzett szervezetek elõ is fordulnak. Igaz, ki sem zárják ezt. Csíkos (tiltott) zónába viszont értelemszerûen nem kerülhet szervezetet jelölõ golyó. Ha egy formalizált elmélet mégis ilyet ír elõ, akkor az a premisszák közti ellentmondást jelent. Ilyenkor, és csakis ilyenkor, a Venn-diagram "nem megrajzolható". A "megrajzolható" Venn-diagramok az adott formulahalmaz logikai modelljeiként szolgálnak. Segítségükkel eldönthetõ, hogy egy mondat (formula) igaz-e az adott premisszák mellett.

1. ábra
Az 5. 1. feltevés grafikus megjelenítése

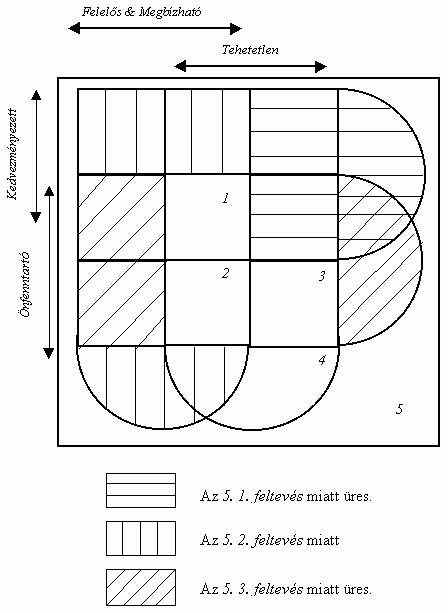
Ha formulahalmazunk (5. 1., 5. 2. és 5. 3. feltevés) nem is biztosítja szervezetek jelenlétét, arról azért tájékoztat, hogy miféle tulajdonságegyüttesekre számíthatunk, ha mégis feltûnik a színen egy szereplõ. A három feltevés fennállása esetén minden szervezet a következõ öt típus (az 1. ábrán: zóna) egyikébe soroltatik:

1. zóna. Tehetetlen, megbízható, felelõs és önfenntartó szerkezetû szervezetek, a kiválasztódás kedvezményezettjei.
2. zóna. Tehetetlen, megbízható, felelõs és önfenntartó szerkezetû szervezetek, nem a kiválasztódás kedvezményezettjei.
3. zóna. Tehetetlen, nem megbízható vagy nem felelõs, de önfenntartó szerkezetû szervezetek, nem a kiválasztódás kedvezményezettjei.
4. zóna. Tehetetlen, nem megbízható vagy nem felelõs, és nem önfenntartó szerkezetû szervezetek, nem a kiválasztódás kedvezményezettjei.
5. zóna. Nem tehetetlen, nem megbízható vagy nem felelõs, és nem önfenntartó szerkezetû szervezetek, nem a kiválasztódás kedvezményezettjei.

A "kiválasztott" szervezetek láthatóan csak az 1. zónában bukkanhatnak fel: megbízhatóan, felelõsen, önfenntartó szerkezettel - és tehetetlenséggel jellemezve. De a premisszák nem biztosítják, hogy minden ilyen jegyekkel rendelkezõ szervezet a kiválasztottak közé is kerül. Ennél nem állít többet Hannan-Freeman (1984) írása sem: a kiválasztott szervezetek nagy tehetetlenségûek.⁸

A Venn-diagram segítségével egy másik módon is bizonyítható az 5. 1. tétel. Próbáljuk a tétel tagadását a premisszahalmazhoz csapni, és mutassuk ki, hogy ez ellentmondásra vezet (reductio ad absurdum)!

5. 1. tétel tagadása. Létezik olyan nem tehetetlen szervezet, amely a kiválasztódás kedvezményezettje.

Ha egy ilyen szervezet léte nem mond ellent a feltevéseknek, akkor a Venn-diagram "megrajzolható" marad: a szervezet létét jelzõ fekete golyónak kerül egy nem tiltott (csíkozatlan) zóna. Egy kedvezményezett, de nem tehetetlen szervezet két zónába kerülhet: a bal szélsõ oszlop két felsõ elemének valamelyikébe. Ezeknek azonban az elsõ két feltevés értelmében (5. 1. és 5. 2. feltevés) lakatlanoknak kell lenniük. Tehát az 5. 1. tétel tagadásával kiegészített premisszahalmaz Venn-diagramja nem megrajzolható. Tehát az 5. 1. tétel tagadása nem igaz: az adott feltevések igazsága mellett nem lehetséges kis tehetetlenségû kiválasztott szervezet. Tehát az 5. 1. tétel igaz.

A kiválasztódás idõt igényel. Vegyük a szervezetek egy hasonló idõben született életkori kohorszát. Tegyük fel, hogy már eltelt annyi idõ, hogy már csak a kiválasztódási elõnyöket hordozók maradtak a porondon. A három feltevés értelmében csakis megbízható, felelõs, önfenntartó szerkezetû és nagy tehetetlenségû túlélõkre számítunk. Ugyanis a szervezeti tehetetlenség szükséges, bár nem elégséges ismérve a kiválasztottságnak. Ebben a tekintetben az 5. 1. tétel hûebben tükrözi Hannan és Freeman eredeti inerciaérvelését, mint a 3. 1. tétel, amely szerint a nagy tehetetlenség önmagában kiválasztódási elõny. Megismételjük: a kiválasztódás számos más tulajdonsággal dolgozik a tehetetlenség mellett. A tehetetlenséget mint a szervezeti üdvösség egyetlen kritériumát beállító inerciaelmélet-értelmezések félreértések. Az újrafogalmazott logikai modell segíthet elsimítani az inercia szerepe kapcsán kirobbant sokéves vitát a szervezetökológia és a szervezetszociológia többi ága között.

A javasolt formalizálás nem zárja ki olyan szerkezetileg szilárd (önfenntartó és nagy tehetetlenségû) szervezetek létét sem, amelyek nem rendelkeznek a megbízhatóság vagy a felelõsség erényeivel. Igaz, ezek a szervezetek nem kerülnek be a kiválasztottak klubjába, hosszú távú életesélyeik nem rózsásak. A javasolt formalizálás (5. 2. feltevés) szerint a szerkezeti önfenntartó képesség csupán lehetõséget, alapot nyújt a megbízható, felelõs mûködéshez. Az "akkor és csak akkor"-tól újra megszabadított második feltevés (5. 2. feltevés) módot ad a lehetõség, valamint a lehetõség megragadása közti szociológiai különbségtételre, s így egy élettelibb formális elmélet megfogalmazására. Míg az elvetett megfogalmazás (4. 2. feltevés) kéretlenül a racionális döntéselmélet vizeire tereli az inerciaérvelést (a szereplõk felismerik és megteszik, ami jó nekik), a javasolt átfogalmazás megfér akár rest vagy tájékozatlan szervezetekkel is. Ezeket a kiválasztódás vonja ki majd a forgalomból, az elméletre rakott megszorító feltevések helyett.

A jogaiba visszahelyezett harmadik feltevés (5. 3. feltevés: a szerkezeti önfenntartó képesség tehetetlenséget von maga után, de nem feltétlenül igaz fordítva) az inerciafogalom egy tágabb értelmezése elõtt nyitja meg a kaput. Például, tehetetlennek nevezhetünk egy bénult, mindennemû rutinszerû tevékenységet (s így: szerkezeti önfenntartást) nélkülözõ halódó szervezetet. Az elvetett 4. 3. feltevés kizárta ezt a lehetõséget. Nem áll szándékunkban most eldönteni, hogy a szervezeti tehetetlenség fogalmának hasznos kiterjesztésérõl van-e szó. De azt jó tudni, hogy a javasolt formalizálás egy ilyen inerciaértelmezéssel is megfér.
 

6. Második újrafogalmazás - a szervezeti tulajdonságok mentén

Az inerciaérvelés egyik sarkalatos eleme, hogy bizonyos szervezeti jegyek idõvel eltûnnek, míg mások elterjednek a szervezetpopulációban. Az uralkodó jegyek feldúsulása az õket hordozó szervezetek elterjedésével történik. Az eddig tárgyalt formalizálások alanyai szervezetek voltak. Azonban az inerciaelmélet nem annyira magukra a szervezetekre, mint az általuk megjelenített tulajdonságokra figyel. A következõ formalizálás ezért a szervezetek helyett a szervezeti tulajdonságokra helyezi a hangsúlyt. Most a fõszereplõ maga a szervezetpopuláció, amelyben a szemügyre vett tulajdonságok felgyûlnek vagy megritkulnak.⁹

Ezen a ponton elhagyjuk a propozicionális logikát, és a tágabb elsõrendû logikát használjuk: a "minden" (" ) jel és változók is fognak szerepelni a következõkben. Az eddigi formulákban a felelõs, megbízható, önfenntartó és tehetetlen kifejezések nullaváltozós predikátumokat jelöltek, amelyek azt állították, hogy a vizsgált szervezet rendelkezik a szóban forgó tulajdonságokkal. Ezúttal az fm, ö és t - tulajdonnevekként - rendre a felelõsség-megbízhatóság, szerkezeti önfenntartó képesség és tehetetlenség tulajdonságokat jelölik majd. Mint kiderül, a tulajdonság alapú megközelítéssel a formalizálás a természetes nyelvi érvelés közvetlen közelében maradhat, így a formalizálás tartalombeli hûsége is könnyebben felmérhetõvé válik. De nem csupán a "felhasználóbarát" modellépítés szándéka késztet minket egy második logikai újrafogalmazásra. Az 5. pontbeli formalizálás a kiválasztódás munkáját a végtermékkel jellemezte: például a megbízhatóság és felelõsség jelenlétével a túlélõk esetében. De szükséges-e feltennünk, hogy minden kiválasztott szervezet hordozza ezeket a jegyeket, miként azt 5. 1. feltétel állítja? Függ-e az inerciatétel igaza az erre a kérdésre adott választól? A következõ formalizálás szerint nem függ.

A kedvezményezett (p) jelölje azt a tényállást, hogy a p-vel jelölt tulajdonság a kiválasztódási folyamat kedvezményezettje.¹⁰ A kiválasztódást a tulajdonság elterjedésével ragadjuk meg. Az elterjed (p) azt a tényállást jelentse, hogy a p-vel jelölt vonás elterjed a vizsgált populációban, azaz a relatív gyakorisága megnõ.

6. 1. definíció. Minden p-re: p akkor és csakis akkor kedvezményezett tulajdonság, ha p elterjed:

Az eredeti három természetes nyelven megfogalmazott feltevés közül az elsõ (2. 1. feltevés) így fejezhetõ ki az adott jelölésekkel:

6. 1. feltevés. A felelõsség és a megbízhatóság kedvezményezett tulajdonság:

A második természetes nyelvi feltevést (2. 2. feltevés) a kétváltozós megkövetel (requires) predikátum segítségével fejezzük ki. Megkövetel (p_1, p₂) jelentse azt, hogy a p₁-gyel jelölt dolog jelenléte megköveteli p₂ jelenlétét.

6. 2. feltevés. A megbízhatóság és felelõsség szerkezeti önfenntartó képességet követel:

Végül a harmadik természetes nyelvi feltevést (2. 3. feltevés) a kétváltozós létrehoz (generates) predikátummal formalizáljuk. Létrehoz (p_1, p₂) oksági viszonyt tételez fel p₁ és p₂ között: ha p₁ (az ok) fennáll, akkor az okozat (p₂) is feltûnik.

6. 3. feltevés. A szerkezet önfenntartó képessége inerciát hoz létre:

A 6. 3. feltevés szerint az önfenntartó képesség tulajdonságával rendelkezõ szervezetek egyszersmind tehetetlenné válnak. Nem állítja viszont, hogy más ok nem vezethet inerciára. Be kell még vezetnünk két háttérfeltevést, amelyek a megkövetel és létrehoz fogalmakat írják körül. 6. 4. feltevés és 6. 5. feltevés szerepe az elõzõ három (6. 1-6. 3.) feltevés összekapcsolása.

6. 4. feltevés. Ha p₁ tulajdonság jelenléte megköveteli p₂-ét, és p₁ elterjed a populációban, akkor p₂ is elterjed:

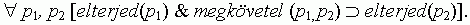
6. 5. feltevés. Ha p₁ tulajdonság megléte p₂-t hoz létre, és p₁ elterjed a populációban, akkor p₂ is elterjed:

Bár az inerciaelméletben szerep jut a folyamatok idõbeliségének, formuláinkban nincs szükség idõváltozóra. De az idõbeliség közvetve mégiscsak jelen van a modellben: a megkövetel és létrehoz predikátumok jelentésébe bugyolálva. A formulákból következõ tétel adódik:

6. 1. tétel. A szervezeti tehetetlenség kedvezményezett tulajdonság:
 

7. Az életesélyek korfüggése - formalizálás a szervezetek mentén

Ha egy elmélet darabjáról már van logikai modellünk, akkor megvizsgálhatjuk, hogy a formulahalmaz megtoldásával esetleg az elmélet más részei vagy más elméletek is megjeleníthetõek-e. Miként a kristályok növekszenek a kristálymag körül, a logikai formalizálás elõsegítheti egy "egyesített" elmélet létrejöttét a meglévõ formális mag körül. Bár az elméletépítés természetes nyelven is történhet, a logika alkalmazása serkentõ hatású lehet. Például segít az elmélet darabok közti információs hézagok feltérképezésében. De segíthet a részek illesztésében is, ha éppen a "túl sok", ellentmondó információ a gond. A 7. és a 8. pont ilyen feladatok megoldásáról tudósít. Hogyan kapcsolódhat a két új formalizálás a szervezetökológia egy új, gyorsan fejlõdõ ágához, amely a szervezeti életesélyek alakulásának életkorfüggését (age dependence) vizsgálja?

A Hannan-Freeman (1984) cikk néhány további feltevést és következtetést is kimondott az inercia életkor- és méretfüggésérõl, és a szervezeti mag (core) megváltoztatásának életkilátásokra gyakorolt hatásáról. Az 1994-es formalizálás ezeket a következtetéseket rendre levezette az új feltevésekkel kiegészített formális modellbõl. Ezeknek az állításoknak egy része azonban nem következik az általunk javasolt, némileg más premisszákra épülõ modellekbõl. Búsuljunk-e vagy örvendezzünk? Meglehet, hogy valószerû, a tapasztalat által igazolt tételeket veszítünk el. Megeshet azonban az is, hogy egy igaz állítást hamis feltevésekbõl vezettünk le. Továbbá egy tétel "elvesztése" nem feltétlenül jelent cáfolatot: esetleg késõbb más, helytálló feltevésekbõl sikerül levezetni a szóban forgó állítást.

Néhány állítás esetében kifejezetten örömteli is lehet, hogy már az nem következik tételként az új inerciamodellekbõl. Ilyen például az Artur Stinchcombe-tól származó ifjúkori esendõség (liability of newness) tétele (Stinchcombe 1965), amely kiemelt szerepet játszott az elmúlt évtizedek szervezetszociológiájában. Az ifjúkori esendõség azt jelenti, hogy a szervezeti életkilátások a születés után javulnak. Hannan-Freeman (1984) egyik feltevése szerint a megbízhatóság és felelõsség rendszerint növekszik, ahogy a szervezet korosodik. Ebbõl és az egy idõváltozóval kiegészített elsõ feltevésbõl az 1994-es formalizálás levezette az ifjúkori esendõség tételének egy erõsebb változatát: az életesélyek szigorúan monoton módon javulnak a korral, azaz a halálozás életkorfüggése negatív. Ezt az inerciatétel közvetett alátámasztásaként lehetett ünnepelni egészen addig, amíg úgy látszott, hogy az empirikus vizsgálatok alátámasztják az ifjúkori esendõséget (például Carroll 1983; Freeman-Carroll-Hannan 1983). Az újabb empirikus eredmények azonban megkérdõjelezik ezt a tételt: a halálozás életkorfüggése sok esetben pozitív (az errõl szóló írások áttekintését lásd Hannan és szerzõtársai 1998). A szervezeti méretváltozások hatását is figyelembe véve, esetenként elavulási (obsolescence) vagy aggkori (senescence) esendõségrõl beszélhetünk (Barron-West-Hannan 1994; Hannan és szerzõtársai 1998). Így annak bemutatása, hogy az ifjúkori esendõség állítása nem feltétlenül következik az inerciaelméletbõl, dicséretes cselekedet lehet.

A következõkben azt vizsgáljuk, hogy a tehetetlenségelmélet új formalizálásaiból vagy azok alkalmas megtoldásából következik-e a szervezeti halálozás akár negatív, akár pozitív életkorfüggése. Ha nem következik, akkor tudni szeretnénk, hogy legalább megférnek-e ezek az állítások a már meglévõ inerciamodellekkel, vagy pedig ellentmondanak a már meglévõ premisszáinknak. Az elméleti takarékosság (parsimony) jegyében igyekszünk mennél kevesebb további információt adni a meglevõ modellekhez. A szervezeti életkor és méret nem szerepel a javasolt új formalizálásokban. Ezért az 5. pontbeli formalizálás szótárát két nullaváltozós predikátummal bõvítjük: jelentse rendre az idõs és a nagy predikátum azt, hogy öreg, illetve, hogy nagyméretû a szemügyre vett szervezet.

Szervezeti halálozás, negatív életkorfüggés. Következik-e az ifjúkori esendõség tétele a szervezet alapú formalizálásból (5. pont), ha a modellt finoman megtoldjuk a korosodásra vonatkozó információval? Elõször is formalizáljuk Hannan-Freeman (1984) elõbb említett állítását, hogy a vizsgált szervezet megbízhatósága és a felelõs volta - tendenciája szerint - erõsbödik az életkorral. Megint érdemes különbséget tenni a lehetõségek, illetve azok megvalósulása között. A kijelentés megítélésünk szerint egy lehetõségre vonatkozik: a korral a szervezeteknek módjuk nyílik megbízható és felelõs mûködést kialakítaniuk. De egyes szervezetek ezt a tapasztalattal és gyakorlattal adódó lehetõséget elszalasztják. Amit állítani lehet: az újonnan alapított szervezetekre még nem jellemzõ a magas megbízhatóságú és felelõs mûködés.

7. 1. feltevés. Az ifjú szervezeteket nem jellemzi magas megbízhatóság és felelõsség:

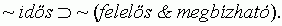
Amibõl a kontrapozíció törvényének¹¹ alkalmazásával adódik, hogy a szervezetek megbízhatósága és felelõs volta erényeivel jellemzett szervezetek idõsek:

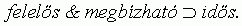
Hannan-Freeman (1984) egy másik állítása szerint a szervezet méretbeli növekedése inerciát okoz. Ez a feltevés majd e pont egy késõbbi részében szereplõ kérdés vizsgálatánál játszik szerepet.

7. 2. feltevés. A nagyméretû szervezetek nagy tehetetlenségûek:

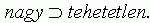
A halálozás negatív életkorfüggése kétféleképpen is kifejezhetõ formális nyelvünk szótárával. Az egyik változat szerint a magas szervezeti életkor jó túlélési esélyt jelent. Az utóbbit a kiválasztódási elõnnyel jelenítjük meg:

7. 3. feltevés. Negatív életkorfüggés (1): ha egy szervezet idõs, akkor a kiválasztódás kedvezményezettje:

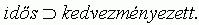
Ez a megoldás azonban ellentétes az 5. pontbeli szervezet alapú formalizálás irályával, ahol a kedvezményezett predikátum az érintett formulák (5. 1. feltevés, 5. 1. tétel) balján, az antecedensben szerepel. Továbbá a 7. 1. feltevés-7. 3. feltevés párosból tételként következik a 2. 1. természetes nyelvi feltevésnek az a formalizálása (3. 1. feltevés), amit az 5. pontban egyszer már jó okkal elvetettünk. A feltámasztott 3. 1. feltevés az érvényben lévõ 5. 1. feltevéssel egyetemben viszont egy erõsen korlátozó állítást eredményez: a kedvezményezettség meglétének szükséges, és egyben elegendõ feltétele a megbízhatóság és a felelõs mivolt:

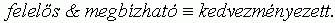
Ezért visszavonjuk a 7. 3. feltevést. Kiemelnénk, hogy a 7. 3. feltevés kiiktatása a formális elméletbõl mérési következményekkel is járhat: a hosszú távú túléléssel (a szervezeti aggkor megérésével) nem operacionalizálható maradéktalanul a kiválasztódási elõny fogalma a jelen inerciaelmélet értelmezés mellett.

A szervezeti halálozás negatív életkorfüggésének egy másik megjelenítési módja:

7. 4. feltevés. Negatív életkorfüggés (2): ha egy szervezet a kiválasztódás kedvezményezettje, akkor idõs:

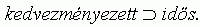
Ez a változat a két másik kiválasztódásra vonatkozó állításhoz (5. 1. feltevés, 5. 1. tétel) hasonló formában mondatott ki. A 7. 4. feltevéssel ellentétben nem köti ki, hogy a magas szervezeti életkor önmagában is elegendõ a kiválasztási elõnyhöz. A 7. 4. feltevés nincs ellentmondásban a már meglévõ premisszákkal. Továbbá az ifjúkori esendõség ebben a második formájában jól megfér az inerciaelméletre adott szervezet alapú modellel. Mi a helyzet a halálozás pozitív életkorfüggésével?

Szervezeti halálozás, pozitív életkorfüggés. Megint kétféle megjelenítést vizsgálunk meg.

7. 5. feltevés. Pozitív életkorfüggés (1): ha egy szervezet a kiválasztódás kedvezményezettje, akkor nem idõs:

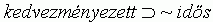
Sajnálatos módon a 7. 1 és 7. 5. feltevéseket az 5. pontbeli premisszákhoz csapva, ellentmondásra jutunk. Az úgynevezett kivágási szabályt (cut rule)¹² alkalmazásával a következõ lemma adódik:

7. 1. lemma:

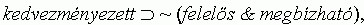
ami ellentmond 5. 1. feltételnek:

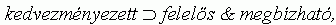
legalábbis amennyiben akad olyan szervezet, amely a kiválasztódás kegyeltje. (Ha nincs ilyen szervezet, akkor ellentmondás sincs, mert akkor a kedvezményezett predikátum jelölte tényállás nem állhat fenn. Ekkor viszont az elmélet okafogyottá válik.) A következtetés irányának megfordításával adódó másik megjelenítés:

7. 6. feltevés. Pozitív életkorfüggés (2): a nem idõs szervezetek a kiválasztódás kedvezményezettjei:

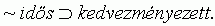
Ez a megoldás nem vezet ellentmondásra. De ugyanaz a tartalmi kifogás vethetõ fel ellene, mint a 7. 3. feltevés ellen: ahogy szemléletünkkel ellenkezõnek találtuk, hogy a hajlott kor önmagában kiválasztódási elõny, úgy vonakodunk elfogadni, hogy az ifjúság elegendõ a kedvezményezettséghez. A halálozás pozitív életkorfüggése tehát nem illeszkedik az 5. pontbeli szervezet alapú inerciamodellhez, legalább-is amennyiben a javasolt minimális szótárbõvítésnél maradunk.¹³

Méretnövekedés az életkorral? Az 1994-es formalizálás egyik mellékterméke volt a monoton növekedés "gyenge" tétele: a szervezetek mérete - átszervezések kivételével - nem csökkenhet. Ez a következmény zavarba ejtõ: ezek szerint minden észrevehetõ méretcsökkenést átszervezésnek kellene minõsíteni. Azt is például, ha a "fûnyíróelvet" alkalmazva minden szervezeti egységet arányosan csökkentenek, és akkor is, ha ez nem vezet szerkezeti változásra. A most vizsgált inerciamodellek javára írható, hogy ez az állítás nem következik a premisszáikból.¹⁴ Ennek belátásához elõször is formalizáljuk a szóban forgó kijelentést. A rendelkezésünkre álló propozicionális nyelven a szervezetek nagyok vagy kicsik (nem nagyok), illetve öregek vagy fiatalok (nem öregek) lehetnek.¹⁵ A vizsgált tétel szerint a szervezet növelheti vagy megõrizheti ifjúkori méretét, de nem mehet össze idõs korára. Vagyis nem lehet az a helyzet, hogy a szervezet, ha ifjú, akkor nagyméretû, és ha agg, akkor apró:

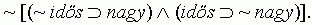
Ami egyenértékû a következõvel:

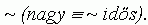
Ha ez az állítás a meglévõ premisszákból következõ tétel, akkor a tagadásának ellentmondásban kell lennie a feltevésekkel (reductio ad absurdum). Az állítás tagadása ("Egy szervezet akkor és csakis akkor nagy, ha nem idõs.") azonban nincs ellentmondásban a többi feltevéssel.¹⁶ Ez azt jelenti, hogy a gondot okozó eredeti (azaz nem tagadott) gyenge monoton méretnövekedést kimondó állítás nem tétel a vizsgált modellben.
 

8. Az életesélyek korfüggése - formalizálás szervezeti tulajdonságok mentén

Most az ifjúkori esendõség, és az aggkori esendõség állításoknak a szervezeti tulajdonságokon alapuló formalizáláshoz (6. pont) való kapcsolatát vizsgáljuk meg. Nem szervezetekrõl beszélünk, hanem szervezeti tulajdonságok populációbeli jelenlétérõl. Tulajdonságoknak nincsen életkoruk, és nincsenek életkilátásaik. Viszont a tulajdonságokat hordozó szervezetek életkilátásai megszabják a sikeres, "kiválasztott" szervezeti vonások elõfordulását a populációban. A szervezeti életesélyek korfüggését ezért megint a kiválasztódási elõnyre hivatkozva jelenítjük meg.

8. 1. feltevés. Pozitív életkorfüggés: az idõs kor nem kedvezményezett tulajdonság:

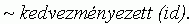
Másodjára a 7. 1. feltevés megfelelõjét formalizáljuk: a szervezetek megbízhatósága és felelõs mivolta növekszik a korral. Szótárunk két kifejezése is alkalmasnak látszik e kapcsolat kifejezésére: a) a szervezetek megbízhatóságának és felelõs voltának megléte magas kort követel meg (requires), illetve b) a magas kor a szervezetek megbízhatóságát és felelõs voltát hozza létre (generates). Noha a két megfogalmazás közti jelentéskülönbség jól érzékelhetõ, nem világos, hogy melyikük alkalmazása milyen elméleti következményekkel jár. A következõ formalizálás a tisztánlátást segíti. Kiderül, hogy a kétféle megoldás által elõálló elméletváltozatok közt tetemes különbség van.

a) változat. Mire vezet a megkövetel predikátum alkalmazása? Jelentse az id és n rende az öregnek lenni és nagynak lenni tulajdonságot.

8. 2. a) feltevés. A szervezetek megbízhatósága és felelõs volta magas kort követel:

A 8. 2. a) feltevés fennállása esetén csakis a koros (id) szervezetek rendelkezhetnek a megbízhatóság és a felelõsség erényével (akár egy elnehezült államszocializmusban). Ekkor azonban kedvezményezett (fm) is fenn forog (a 6. 1. feltevés miatt), amire a 6. 1. definíciót alkalmazva a következõre jutunk:

Ebbõl viszont a 6. 4. feltevés által

adódik. A 6. 1. definíció újbóli alkalmazásával a következõ tételt kapjuk.

8. 1. tétel. Negatív életkorfüggés: az idõs kor kedvezményezett tulajdonság:

A 8. 1. tétel ellentmond a 8. 1. feltételnek. Tehát a megkövetel predikátum alkalmazása esetén modellünk a halálozási esély negatív korfüggését kimondó tételre vezet. Ha a magas kor feltételezi a kiválasztódási elõnyt jelentõ megbízhatóság-felelõsség meglétét, akkor az öreg szervezetek talpon maradási esélyei nem lehetnek rosszabbak az újoncokéinál. (E tétel bizonnyal nem igaz biológiai organizmusokra.)

b) változat. Mire vezet a létrehoz predikátum alkalmazása?

8. 2. b) feltevés [a 8. 2. a) feltevés helyett]. Az idõs kor megbízhatóságot és felelõs voltot hoz létre.

Mivel esetenként különféle hatások hozhatnak létre, "generálhatnak" egy adott kimenetelt (itt: a szervezetek megbízhatóságát és a felelõs voltát), a létrehoz predikátum alkalmazása elõdjénél kevésbé szûkkeblûen bánik az ifjú szervezetekkel. Az idõseknél garantálja, a fiataloknál megengedi a megbízhatóságot és a felelõs mivoltot. A 6. 1. definícióból, a 6. 1-6. 5. feltevésekbõl és a 8. 2. b) feltevésbõl álló formulahalmaz ellentmondásmentes marad akár a 8. 1. feltevést, akár a 8. 1. tételt adjuk hozzá (ennek demonstrálására még visszatérünk). Vagyis a 8. 2. b) feltevéssel kiegészített feltevéshalmazból nem következik tételként a halálozásnak sem negatív (8. 1. tétel), sem pozitív (8. 1. feltevés) életkorfüggése. Szerencsére, mondhatjuk, mivel mindkét esetben kimutatott jelenségrõl van szó. Így bármelyik változat tétellé emelésével a modell kizárná a másik elõfordulását. Az elmélet további építése szempontjából kellemes helyzetbe jutottunk: a formális inerciamodell különbözõ korfüggési mintázatokkal fér meg. Hogy mikor melyik érvényes, illetve még milyen más (akár nem monoton) életkorfüggés adódhat, az további változók alakulásától függ (Hannan 1998).

Végezetül vizsgáljuk meg, hogy mi mondható a nem kívánt méret növekedési tételrõl a szervezeti tulajdonságokra épülõ modellben. Következik-e a premisszákból, vagy mint reméljük: nem. Formalizáljuk (a 7. 2. feltevés analógiájára), hogy a nagy méret inerciával jár:

8. 3. feltevés. A nagy méret tehetetlenséget hoz létre.

Ezúttal a populációban jelen lévõ, illetve hiányzó tulajdonságokra hivatkozva kell kifejeznünk azt, hogy a szervezet mérete a korral nem csökkenhet. Újra kiemelnénk, hogy a szervezeti méret gyenge monoton korfüggése a dichotóm életkor (nem öreg-öreg) és méret (nem nagy-nagy) tulajdonságok négy lehetséges kombinációja közül csak azt a párosítást zárja ki, amikor a fiatal szervezetek nagyok, de idõsen kicsik lesznek. A populáció szintjén: ha a fiatalnak lenni tulajdonság jelenléte azt feltételezi, hogy a nagy szervezetméret jellemzõ a populációra, akkor öregnek lenni tulajdonság jelenlétének is nagy szervezetméretet kell jelentenie. A ifjúnak lenni tulajdonságra az if elnevezést bevezetve¹⁷ ez így fejezhetõ ki a rendelkezésünkre álló szótárral:

8. 4. feltevés

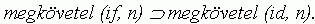
E formula tagadása így is írható:¹⁸

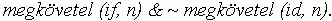
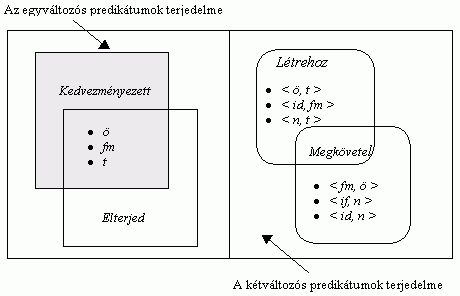
Azaz: megeshet, hogy az ifjúkor populációbeli jelenléte nagy méretet von maga után, míg az idõs koré nem. Ez az állítás nincs ellentmondásban a megtartott többi formulával. A 8. 4. feltevés, valamint a 8. 2. b) feltevés korábban beígért összeférhetõségét a tulajdonság alapú modellel a 2. ábrán szemléltetjük. Megint: az 1. ábra kapcsán lefektetett szabályokat követve, megpróbálunk egy Venn-diagramot rajzolni, amelyen formalizálásunk összes formulája megjeleníthetõ ("igaz" kijelentések). Ha ez sikerül, úgy formulahalmazunk ellentmondásmentes. Mivel most kétváltozós predikátumok is szerepelnek a formalizálásban, ezért némileg másként kell eljárnunk, mint az 1. ábra esetében tettük. Ezúttal a predikátumokat a terjedelmükkel (extension) jelenítjük meg.¹⁹ Jelölje <a, b>, hogy az a-val és b-vel jelölt dolgokból képzett rendezett pár kielégíti a szóban forgó kétváltozós predikátumot. A 2. ábra formuláink egy modelljét jeleníti meg. A modell "megrajzolhatósága" azt jelenti, hogy formulahalmazunk ellentmondásmentes. Tehát a halálozás pozitív életkorfüggése megfér modellünkkel, a nem kívánt méretnövekedésre vonatkozó kijelentés pedig (mint reméltük) nem tétele modellünknek. Hangsúlyoznánk, hogy a halálozás pozitív korfüggését (aggkori esendõség) nem bizonyítottuk. Ez nem következik a formulákból. De a kínált inerciamodell legalábbis nyitva hagyja az ajtót egy olyan lehetséges bõvített elmélet (további információ bevitele) elõtt, aminek a kérdéses aggkori esendõség már logikai következménye lehet.
 

Összefoglalás

Az írás két új formalizálást adott a szervezetökológia inerciaelméletére, egyet a szervezetek, egyet a populáció szintjére figyelve. A két modell némileg eltérõ megfontolásokból vezeti le az inerciatételt. A logikai formalizálás elõnye, hogy áttekinthetõ, feltevésrõl feltevésre haladva szemügyre vehetõ módon jeleníti meg az érvelést. Így az olvasónak módjában áll mérlegelni, hogy formuláink helyesen ragadják-e meg a formalizálni kívánt állításokat. Ha ez a helyzet, úgy bebizonyítottuk, hogy az inerciaelméletnek létezik legalább két logikailag helytálló olvasata. Ellentétben a vizsgált 1994-es formalizálással, a két új modell a természetes nyelvi elmélet érvényességi körének szûkítése nélkül vezeti le az inerciatételt.

2. ábra
A modell grafikus megjelenítése

Egy másik fontos lépés a formalizálásoknak a tágabb szervezetökológiai elméletbe való beágyazása. Ezt a feladatot a szervezeti halálozás életkorfüggése kapcsán végeztük el.²⁰ Az 1994-es formalizálásból tételként következett az azóta megkérdõjelezett érvényességû ifjúkori esendõség tétel (a halálozás negatív életkorfüggése). Kimutattuk, hogy a szervezeti tulajdonságokra alapuló formalizálás jól megférhet mind az ifjúkori, mind az aggkori esendõséggel (pozitív és negatív életkorfüggéssel). Ez szabadságot ad a további formális elméletépítés számára: döntsék el a felgyûlõ tapasztalati tudáson alapuló további premisszák, hogy mikor melyik érvényes.

Ha egy logikai formalizálásból valami képtelen állítást lehet levezetni, akkor vagy a természetes nyelvi elmélet rossz valahol, vagy pedig legalább egy feltevést félreformalizáltunk. Így örömhír, hogy egyik formalizálásunkból sem következik az a tapasztalattal ellenkezõ kitétel, hogy a szervezetek mérete kizárólag átszervezéssel csökkenhet. Ez azt jelzi, hogy nem az inerciaelmélet, hanem annak 1994-es formalizálás által adott olvasata vezetett erre a nemkívánatos tételre.

A tartalom és a formális megjelenítés kapcsolata örökzöld módszertani téma. A megjelenítés hûségének egyik mércéje, hogy a formulákból milyen további következtetések vonhatók le, hogyan "viselkedik" a modell, ha további információt adagolunk hozzá. A logikai formalizálás megenged némi célzott találgatáson alapuló játszódást (Hannan 1998; Péli 1997b): milyen új tétel változatok következnek, ha különféle premisszákot adunk az eleméleti maghoz. A formalizáláskor célul tûztük ki, hogy a modelljeink egyszerûek legyenek. Ezért bennünket is meglepett, hogy mennyire különbözõ szociológiai következményekre vezet ezeknek a nem túl bonyolult modelleknek már szerény megtoldása is. A formális mag (az inerciaelmélet) sokban megszabta a hozzáadott információ formalizálásának módját: bizonyos változatokat ki kellett zárni, mert a következmények ellentmondottak a tágabb szervezetökológia elmélet valamely sarkalatos kitételének (például annak, hogy a megbízhatóság és a felelõs mivolt rendszerint erõsödik az életkorral). A két bemutatott inerciaformalizálás különbözõ lehetséges pályákat jelöl ki az elméletépítés számára. Ez a tény újabb érvet szolgáltat, hogy miért is jó, ha különféle logikai modelljeink vannak ugyanarra az elméletre, különösképpen gyorsan fejlõdõ területeken. A dolgok rendje szerint való, hogy a folyamatosan gyûlõ empirikus tudás megkérdõjelezi az elméletek egyes korábbi megállapításait. Idõrõl idõre az elmélet magja is újragondolásra szorul. Ilyenkor jól jön, ha a kutató többféle, világosan kifejtett olvasat közül választhatja ki a továbblépést lehetõvé tevõ változatokat. A logikai formalizálás segíti a lehetséges pályák feltérképezését.
 

Hivatkozások

Barnett, W. P.-G. R. Carroll 1995. Modelling Internal Organizational Change. Annual Review of Sociology, 21, 217-236.

Barron, J. N.-M. D. Burton-M. T. Hannan 1996. The Road Taken: Origins and Evolution of Employment Systems in Emerging Companies. Indusrtial and Corporate Change, Vol. 5(2).

Barron, D. N.-E. West-M. T. Hannan 1994. A Time to Grow and a Time to Die: Growth and Mortality of Credit Unions in New York, 1914-1990. American Journal of Sociology, 100, 381-421.

Barwise, J.-J. Etchemendy 1990. The Language of First-order Logic. Stanford University, CA. CSLI 23.

Carroll, G. R. 1983. A Stochastic Model of Organizational Mortality: Review and Reanalysis. Social Science Research, 12, 303-329.

Freeman, J.-G. R. Carroll-M. T. Hannan 1983. The Liability of Newness: Age Dependence in Organizational Death Rates. American Sociological Review, 48, 692-710.

Gamut, L. T. F. 1991. Logic, Language and Meaning. Vol. 1-2. Chicago: Chicago University Press

Hannan, M. T. 1998. Rethinking Age Dependence in Organizational Mortality: Logical Formalizations. American Journal of Sociology, 104, 85-123.

Hannan, M. T -G. R. Carroll.-S. Dobrev-J. Han 1998. Organizational Mortality in European and American Automobile Industries, Part I. Revisiting the Effects of Age and Size. (Forthcoming)

Hannan, M. T.-J. Freeman 1977. The Population Ecology of Organizations. American Journal of Sociology, 82, 929-964.

- - 1984. Structural Inertia and Organizational Change. American Sociological Review, 49, 149-164.

- - 1986. Where Do Organizational Forms Come From? Sociological Forum, 1, 50-72.

- - 1989. Organizational Ecology. Cambridge MA.: Harvard University Press

Hannan, M. T.-J. Freeman-M. D. Burton-J. N. Barron 1996. Inertia and Change in the Early Years: Employment Relations in Young High Technology Firms. Industrial and Corporate Change, Vol. 5(2).

Kamps, J.-Pólos, László 1999. Reducing Uncertainty: A Formal Theory of Organizations in Action. (Forthcoming)

Kreps, D. M. 1996. Markets and Hierarchies and (Mathematical) Economic Theory. Industrial and Corporate Change, 5, 561-596.

Mintzberg, H. 1979. The Structuring of Organizations. Englewood Cliffs: Prentice-Hall

Nelson, R. R.-S. G. Winter 1982. An Evolutionary Theory of Economic Change. Cambridge M A.: Belknap Press of Harvard University

Péli Gábor 1997a The Niche Hikers Guide to Population Ecology: A Reconstruction of Niche Theory Using Logic. In: A. E. Raftery (ed.) Sociological Methodology. Cambridge: Blackwell, 1-46.

- 1997b Rejoinders: Reply: Intuition and the Formal Approaches. In: A. E. Raftery (ed.) Sociological Methodology. Cambridge: Blackwell, 159-164.

- 1998. The Cricket and the Ant: Organizational Tradeoffs in Changing Environments. Groningen. Kézirat.

Péli Gábor-J. Bruggeman-M. Masuch-B. Ó Nualláin 1994. A Logical Approach to Organizational Ecology: Formalizing the Inertia Fragment in First-Order Logic. American Sociological Review, 59, 571-593.

Péli Gábor-M. Masuch 1997. The Logic of Propagation Strategies: Axiomatizing a Fragment of Organizational Ecology in First-Order Logic. Organization Science, 8 (3) 310-331.

Péli Gábor-B. Nooteboom 1999. Market Partitioning and the Geometry of the Resource Space. American Journal of Sociology, Vol, 104, 148-169.

Podolny, J. M. 1993. A Status-Based Model of Market Competition. American Journal of Sociology, 98, 829-872.

Pólos László-Ruzsa Imre 1987. A logika elemei. Budapest: Tankönyvkiadó

Pólos László-M. T. Hannan-G. R. Carrol. 1998. Forms and Identities: On the Structure of Organizational Forms. Amszterdam-Stanford-Berkeley. Kézirat.

Pólos László-Péli, Gábor-M. T. Hannan-G. R. Carroll 1999. Structural Inertia and Organizational Change Revisited. Kézirat.

Stinchcombe, A. L. 1965. Social Structure and Organizations. In: J. G. March-Rand McNally (eds.) Handbook of Organizations. Chicago, 142-193.
 

* Ezúton szeretnénk köszönetet mondani az Alfred P. Sloan Foundation-nek a támogatásért és a Stanford Graduate School of Business Faculty Trustnak, amiért e kutatás sikerét elõsegítette. Köszönjük Glenn Carroll, Bill Barnett, Jaap Kamps és Tomas Klos az írást lényegesen jobbá tévõ javaslatait. A megmaradó hibákról kizárólag a szerzõk tehetnek.
1. Megemlítünk néhány angol nyelvû szervezetszociológiai tárgyú logikai és matematikai formalizálást: Hannan (1998), Kamps-Pólos (1999), Péli (1997a; 1998), Péli-Masuch (1997), Péli-Nooteboom (1999), Pólos-Hannan-Carroll (1998).
2. Idõrõl idõre meg is kapja a szervezetökológia a szociálidarwinizmus bélyegét. Alaptalanul, mivel nem a biológiai tudásanyag társadalmi közegbe való "behelyettesítése" a célja, hanem megközelítési módokat vesz át a biológiai kutatásoktól.
3. Egy sor angol kifejezésnek nincs kiforrott magyar megfelelõje. A szakma ilyen helyzetekben sokszor egy magyar képzõ hozzáillesztésével fordít. Mi mégis Kazinczy és Kosztolányi útmutatását követjük: minden angol szakszóhoz magyar megfelelõt kerítünk, vállalva, hogy esetenként még "megérzik rajtuk a vad íz". Azt reméljük, hogy a rendszeres használat majd kijegecesíti pontos szakmai jelentésüket.
4. A három feltevés és a tétel így hangzik angol eredetiben:
Assumption 2. 1. Selection in populations of organizations in modern societies favors forms with high levels of accountability and high reliability of performance.
Assumption 2. 2. Accountability and reliability require that organizational structures be highly reproducible.
Assumption 2. 3. High levels of reproducibility of structure generate strong inertial pressures.
Theorem 2. 1. Selection within populations of organizations in modern societies favors organizations whose structures have high inertia.
5. Három tankönyv, amely bevezetést nyújt a logikába: Barwise-Etchemendy (1990), Gamut (1991), Pólos-Ruzsa (1987). Cikkünk ez utóbbi, magyar nyelvû tankönyv Magyarországon meghonosodott logikai jelölésrendszerét követi. Zárójelben közöljük a másik két könyv, és a hivatkozott szociológiai témájú logikai formalizálás cikkekben használt megfelelõ jelöléseket is. "Minden": 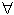; "létezik": 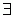; "nem", negáció: 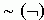; "és", konjunkció: 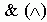; "vagy", diszjunkció: 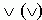; "ha, ... akkor", impliká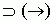ció: ; "akkor és csak akkor" biimplikáció: .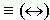
6. Az 1994-es formalizálás egy további - az elemzett érvelést ugyan nem érintõ - problémás pontja, hogy a késõbbiekben minden további tételt szigorúan monoton függvények alkalmazásával vezet le. Például ha az önfenntartó képesség (A) növekszik, akkor a tehetetlenség (B) is nõ. Csakhogy a szigorúan monoton függvények invertálhatóak, és az inverzük ugyancsak szigorúan monoton lesz. Ez annyit tesz az elõbbi példánál maradva, hogy A akkor és csak akkor nõ, ha B nõ. Vagyis de facto "akkor és csak akkor"  összefüggés áll fenn A és B között az összes ilyen jellegû formulában, akár megjelenik ez a jelölésben, akár nem. Ez fölöslegessé teszi a következtetési irányokról szóló elemzéseket az 1994-es formalizálásban.
7. Ha jól körülnézünk, találhatunk hosszú távon túlélõ, ám kis tehetetlenségû szervezeteket. Az ellenpéldák arra utalnak, hogy az 5. 1. tétel legalább egy premisszája nem minden körülmények között állja meg a helyét. Vagyis az inerciaelmélet (mint az elméletek általában) korlátozott érvényességû.
8. Új (így gyakran kis inerciájú) szervezetek tömeges megjelenése a populációban nyilván összerondíthatja a képet. De a cél a hasonló idõpontban született szervezetek életpályáinak összevetése, eltérõ inerciáik függvényében.
9. Mivel végig ugyanarról a tetszõlegesen választott populációról lesz szó, ezért szükségtelen (bár megtehetõ), hogy minden egyes feltevésben formálisan is utaljunk a jelenlétére egy predikátummal.
10. Emlékeztetünk, hogy a korábban szereplõ kedvezményezett nullaváltozós predikátumot kifejezetten szervezetekre vonatkoztattuk.
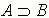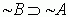11. A kontrapozíció törvénye szerint  és  logikailag egyenértékûek.
12. A kivágási szabály szerint 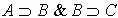 következménye  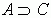(vagyis B "kivágható" a képbõl).
13. Egy másik lehetõség a 7. 5 és a 7. 6. feltétel megtartása és a 7. 1. feltétel elvetése lehetne. Ez azonban az inerciaelmélet egy sarkalatos pontjának feladását jelentené.
14. Megjegyezzük, hogy a modell alkalmas finomításával a hivatkozott 1994-es formalizálásból is kiiktatható e nem kívánatos következmény: a szöveg beható elemzésébõl kitetszik, hogy a tétel premisszái ceteris paribus ("feltéve, hogy a többi hatás nem változik", "other things being equal") jellegû állítások. A tétel onnan adódik, hogy a formalizálás ilyen további hatásokat - információ hiányában - nem vett figyelembe.
15. Egy idõváltozó bevezetésével valamivel bonyolultabb, de pontosabb, elsõrendû logikára épülõ modellhez jutunk. Ez azonban hasonló eredményre vezetne. Továbbá az átszervezéseket (reorganization) sem szerepeltetjük modellünkben. Ezek beiktatása szintén nem befolyásolná a végeredményt. Érdeklõdés esetén a szerzõk szívesen bemutatják a vonatkozó formalizálásokat.
16. Zavarónak tûnhet, hogy a fenti állítás szervezetszociológiai szempontból aligha ír le tipikus helyzetet. A jelen teszt szempontjából azonban elgendõ, hogy nem lehetetlen esetre utal.
17. Mivel id egy tulajdonság "tulajdonneve" (öregnek lenni), nem predikátum, ezért nem is alkalmazhatjuk rá a "tagadás" mûveletet. Ezért vezetünk be egy külön jelölést (if) az ellentétes tulajdonságra.
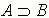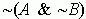18.  egyenértékû a következõvel: . Azaz egy következtetésnél nem fordulhat elõ, hogy az elõtag igaz volta mellett az utótag hamis.
19. Egy egyváltozós predikátum terjedelmét azon dolgok adják, amelyek behelyettesítésével adódó kijelentések igazak a szóban forgó elméletben. Egy kétváltozós predikátum terjedelmét a dolgoknak azok a párosításai alkotják, amelyeket behelyettesítve igaz kijelentésre jutunk.
20. Egy készülõben lévõ írásunk további kapcsolódási pontokat elemez (Pólos-Péli-Hannan-Carroll 1999).