Kockázatkerülõ, kockázatsemleges és kockázatkedvelõ döntéshozók elemi haszonfüggvénye
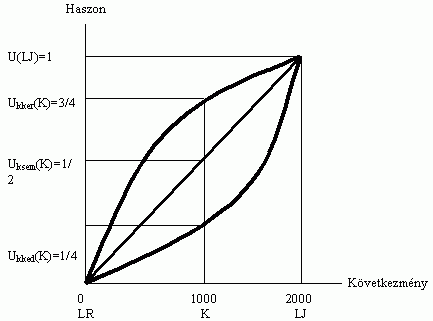
Tanulmányunkban a kockázatvállalással és kockázatkerüléssel kapcsolatos társadalmi attitûdök empirikus vizsgálatára teszünk kísérletet. Elõször röviden bemutatjuk a problémának a racionális döntések elmélete által kínált analitikus megközelítését, majd röviden érintünk néhány - a kísérleti közgazdaságtanból és döntéspszichológiából származó - olyan megállapítást, amelyeket a bizonytalanság és a kockázat körülményei közötti döntésekkel kapcsolatos empirikus vizsgálatok alapján fogalmaztak meg. Ezt követõen bemutatjuk a kockázatvállalás operacionalizálási kísérletét, melyet kérdõíves adatfelvételi módszer keretében alkalmazunk.
A kockázatvállalási attitûdöt a szokásos módon térképezzük fel: azt kérjük a megkérdezettektõl, hogy válasszanak egy kisebb összegû biztos és egy nagyobb összegû kockázatos nyeremény között. Elméleti modelljeinkbõl és korábbi empirikus kutatásokból kiindulva, hipotéziseket fogalmazunk meg arra vonatkozóan, hogy a vizsgált döntési helyzetben milyen tényezõk hatnak a ténylegesen megszületõ döntésekre. Adataink alapján ezeket a hipotéziseket ellenõrizzük. Gondolatmenetünket rövid összegzés zárja.
Tanulmányunk újdonsága, hogy a magyar szakirodalomban
- ismereteink szerint - még nem számoltak be efféle
empirikus kísérletekrõl. Az pedig, hogy a vizsgálatot
viszonylag nagymintás, kérdõíves adatfelvétel
alapján végezzük, tudomásunk szerint a nemzetközi
szakirodalomban is ritkaságszámba megy.
A kockázattal szembeni attitûd analitikus modellje
Bizonyosság, bizonytalanság, kockázat
A racionális döntések elméletében a döntési helyzetek egyik osztályozása alapján különbség van a döntés szempontjából releváns környezeti állapotokra (világ-állapotokra), s ennek következtében a cselekvési alternatívák következményeire vonatkozó teljes és hiányos informáltság között (Elster 1986: 5). Amikor például egy gazdának két vetõmag közül kell választania, számolnia kell azzal, hogy a jövõ évben várható terméseredmény részben a következõ év idõjárási állapotaitól függ. Ez viszont nem jelezhetõ elõre teljes bizonyossággal. Gyakorlatilag az összes valóságos helyzet ebbe a típusba tartozik, néhány azonban közülük erõsen megközelíti a teljes bizonyosság határesetét. Teljes bizonyosságról akkor beszélünk, ha a döntéshozó pontosan tudja, hogy melyik világállapot (s milyen következményhalmaz) áll elõ: az egyik világállapot bekövetkezési valószínûsége egy, az összes többié nulla.
Fejtsük ki a fenti egyszerû példát (Elster
1995: 34-35; 1986: 6). Kétféle vetõmag van, A
és B, és kétféle lehetséges idõjárás
(világállapot), Jó és Rossz,
melyekrõl információink alapján feltesszük,
hogy bekövetkezésük egyformán valószínû
(50-50%). E kétféle idõjárás esetén
a vetõmagok hozamából nyerhetõ lehetséges
jövedelmeket mutatja az 1. táblázat. A zárójelben
levõ számok a gazdának a különbözõ
jövedelmi szintekbõl származó hasznát
mutatják. A haszonértékek tükrözik a pénz
csökkenõ határhasznának általános
tendenciáját: minden újabb dollárnyi jövedelem
egyre kisebb haszonnövekményt képvisel.
1. táblázat
Következménymátrix bizonytalanságban hozott
döntés esetén
|
|
|
|
||
| jövedelem (dollár) | haszon (U) | Jövedelem (dollár) | haszon (U) | |
| Jó |
|
|
|
|
| Rossz |
|
|
|
|
| Átlag |
|
|
|
|
Az olyan döntési helyzetek, amelyekben az információk hiányosan állnak az érdekeltek rendelkezésére, a kockázat és a bizonytalanság fogalmaival jellemezhetõk. A tág értelemben vett bizonytalanság esetén a döntéshozó tisztában van azzal, hogy több világállapot következhet be, s tudja azt is, hogy melyek. Példánknál maradva: tág értelemben vett bizonytalanság esetén a gazda tisztában van azzal, hogy kétféle idõjárás következhet be: Jó és Rossz. Ezen belül kockázatról beszélünk azokban az esetekben, ahol a döntéshozók a világállapotokhoz számszerû (objektív vagy szubjektív) bekövetkezési valószínûségeket tudnak rendelni. A szûk értelemben vett bizonytalanság esetén viszont a döntéshozók nem ismerik a szóban forgó valószínûségi értékeket. Ha a gazda - többé-kevésbé megalapozottan - 50-50 százalékos valószínûséggel számol a Jó és a Rossz idõjárás bekövetkezésével, akkor a kockázat körülményei között hozza meg döntését, ha viszont nem rendel semmilyen valószínûségi értéket a világállapotokhoz (vagy másképpen: nem képes semmilyen valószínûségi becslést kialakítani a világállapotok bekövetkezésére), akkor a szûk értelemben vett bizonytalanságban.
Ez egyike azoknak a kérdéseknek, amelyben nincs teljes
egyetértés a hagyományos és a modern (bayesianus)
döntéselmélet hívei között, habár
egyre több jel mutat a modern álláspont elfogadottságára.
Utóbbiak szerint (Hirsleifer-Riley 1998: 27-29.) ugyanis egyrészt
minden helyzetben képesek a racionális cselekvõk
többé-kevésbé megbízható (puhább
vagy keményebb) valószínûségi becsléseket
kialakítani a rendelkezésükre álló információk
(tudás) alapján a világállapotok bekövetkezésére,
másrészt: minden valószínûségi
becslés - többé-kevésbé - szubjektív
természetû. A bizonytalanság és a kockázat
közti különbség eltûnik: a megfelelõ
normatív döntési kritérium szerint azt a cselekvési
alternatívát kell választania a racionális
cselekvõnek, amelyik révén a (szubjektíve)
várható hasznosság maximalizálható.
Egy cselekvés várható hasznosságát azon
hasznosságok súlyozott átlagaként határozhatjuk
meg, amelyekkel a kérdéses cselekvések következményei
a különbözõ világállapotok bekövetkezése
esetén járnak. A súlyokat a világállapotok
bekövetkezési valószínûségei adják.
Kockázatkerülés, kockázatsemlegesség, kockázatkedvelés
A kockázattal kapcsolatos attitûd értelmezéséhez
térjünk vissza az 1. táblázathoz! Világos,
hogy B vetõmagnak magasabb a várható hozama,
s így magasabb várható jövedelmet jelent. Ez
azonban nem jelenti feltétlenül azt, hogy A-nak magasabb
a várható hasznossága, s így a racionális
döntéshozó ezt választaná. Ha mondjuk
20 000 dollár jövedelemre mindenképpen szüksége
van a megélhetéshez, akkor bolond lenne olyan vetõmagot
választani, amely 50 százalékos eséllyel kockára
teszi a megélhetését. Mindez nem más, mint
a pénz csökkenõ határhasznának speciális
esete, amibõl következik, hogy a várható jövedelem
haszna nagyobb, mint a jövedelem várható haszna (Elster
1986: 6; Varian 1991: 278-280). Példánkban:
U[(50 000/2+15 000)/2]>[U(50 000)+U(15 000)]/2=48>41,5.
Általánosítsuk a példában szereplõ összefüggéseket (Hirshleifer-Riley 1998: 34-47; Morrow 1994: 36-37). Vegyük a következõ egyszerû döntési helyzetet: a döntéshozó választhat A és B között. Ha A-t választja, biztosan megkapja a K közepes (átlagos) következményt, ha viszont B-t, akkor p valószínûséggel megkapja a legjobb LJ következményt, és (1-p) valószínûséggel a legrosszabb LR következményt. Konkrétabban: tegyük fel, hogy a döntéshozó a következõ döntési problémával találkozik: ha A-t választja, akkor kap 1000 forintot, ha B-t, akkor p valószínûséggel kap 2000 forintot, vagy (1-p) valószínûséggel semmit. Világos, hogy A és B közti választás mindenekelõtt p értékétõl függ: ha p közel van 1-hez, akkor várhatóan B-t, míg ha p közel van nullához, akkor a racionális egyén várhatóan A-t fogja választani. A két szélsõ érték között viszont léteznie kell olyan pontnak, ahol a döntéshozó számára közömbös A és B. Az ehhez a ponthoz tartozó p* valószínûségi értékrõl pedig bebizonyítható, hogy megfelel K következmény kardinális hasznossági értékének3: U(K) = p*. Mondjuk sikerült megállapítanunk, hogy a döntéshozó akkor közömbös A és B között, ha p*=3/4. Ezt a döntéshozót kockázatkerülõnek nevezzük. Általánosabban: kockázatkerülõnek nevezzük azt a döntéshozót, aki a biztos alternatívát szigorúan elõnyben részesíti az azonos várható értékû kockázatos alternatívával szemben, kockázatkedvelõnek nevezzük azt a döntéshozót, akinek a fenti esetben fordított a preferenciája, míg a kockázatsemleges döntéshozó közömbös az azonos várható értékû biztos és kockázatos választási lehetõségek között (Hirshleifer-Riley 1998: 42).
Az 1. ábra három elemi haszonfüggvényt mutat: kockázatkerülõ (Ukker), kockázatsemleges (Uksem) és kockázatkedvelõ (Ukked) döntéshozó elemi haszonfüggvényét. A vízszintes tengelyen a következményeket, a függõleges tengelyen a hasznokat ábrázoljuk. Mindhárom döntéshozónak ugyanakkora haszna származik a legjobb és a legrosszabb következménybõl. A kockázatsemleges döntéshozó példánkban p*=1/2 valószínûség mellett lesz közömbös A és B között. A kockázatsemleges elemi haszonfüggvénye (Uksem) lineáris, mert az õ esetében a következmény várható haszna egyenlõ a várható következmény hasznával. A kockázatkerülõ döntéshozó valamilyen 1/2<p<1 valószínûség mellett lesz közömbös A és B között, attól függõen, hogy milyen mértékben kerüli a kockázatot. A kockázatkerülõ elemi haszonfüggvénye (Ukker) konkáv, mert az õ esetében - a korábban mondottakkal összhangban - a következmény várható haszna kisebb a várható következmény hasznánál. A kockázatkedvelõ valamilyen 0<p<1/2 valószínûség mellett lesz közömbös A és B között, attól függõen, hogy milyen mértékben kedveli a kockázatot. A kockázatkedvelõ haszonfüggvénye (Ukked) konvex, mert az õ esetében a következmény várható haszna nagyobb a várható következmény hasznánál4.
1. ábra
Kockázatkerülõ, kockázatsemleges és
kockázatkedvelõ döntéshozók elemi haszonfüggvénye
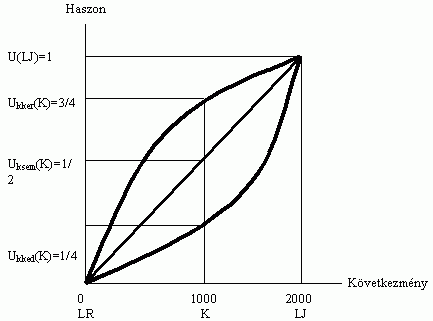
A fent bemutatott standard döntéselméleti modellek egyik feltevése, hogy az egyéni preferenciák és döntések függetlenek a döntéshozók kiinduló helyzetbeli vagy aktuális - tág értelemben vett - vagyoni állapotától5. Az olyan modellek, mindenekelõtt az iménti lábjegyzetben említett kilátáselmélet, amelyek részben feloldják a szóban forgó feltevést, a következõ posztulátumokon nyugszanak: 1. a haszonértékeket nem a cselekvõk vagyoni helyzetéhez, hanem olyan állapotváltozásokhoz (veszteségekhez és nyereségekhez) kell rendelni, amelyek valamilyen referenciaponthoz (például a status quóhoz) képest következnek be; 2. azok a változások, amelyek a helyzet rosszabbodását okozhatják, fontosabbak a cselekvõk számára, mint azok, amelyek javulást eredményezhetnek. A kilátáselmélet kétféle függvényt használ a döntések jellemzésére: 1. az értékfüggvényt, amely felváltja a standard döntéselmélet elemi haszonfüggvényét; 2. a döntésisúly-függvényt, amely a valószínûségeket döntési súlyokká alakítja.
Ha a veszteségek és nyereségek értékelését
koordinátarendszerben ábrázoljuk, akkor az itt vizsgált
elméletbõl és az ezt alátámasztó
empirikus adatokból6 az következik,
hogy az értékfüggvény meredekségének
abszolút értéke nagyobb lesz a veszteségek,
mint a nyereségek tartományában, miközben a nyereségek
és veszteségek növekedésével mind a nyereségek,
mind a veszteségek határhaszna csökken. Egyszerûbben:
az értékfüggvény S-alakú, a nyeremények
tartományában konkáv, a veszteségek tartományában
viszont konvex, továbbá elsõsorban veszteségkerülést
mutat, mivel a veszteségfüggvény meredekebb, mint a
nyereségfüggvény. A 2. ábra egy elképzelt
értékfüggvényt mutat be.
A kockázattal szembeni attitûd empirikus modellje
Általános keretek
Tanulmányunkban a kockázattal szembeni attitûd társadalmi-demográfiai és más meghatározóit keressük. Alapkérdésünk az, hogy mitõl függ a döntéshozók kockázatvállalási hajlandósága. Milyen társadalmi-demográfiai és egyéb tényezõk befolyásolják a döntéshozók kockázattal szembeni attitûdjét? Kiinduló modellünkben a kockázattal szembeni attitûd függ a nyeremény nagyságától, valamint a döntéshozó jövedelmi helyzetétõl, foglalkozásától, iskolai végzettségétõl, életkorától és nemi hovatartozásától:
KSZA = f(NYN, Jov, Fogl, iskola, kor, Nem),
ahol
Az empirikus elemzés során abból indulunk ki, hogy
a fent említett változóknak már az elemzés
kezdetén eltérõ a státusuk. Tekintettel arra,
hogy a nyereményeket/veszteségeket a jövedelem emelkedéseként
vagy csökkenéseként értelmezzük, elõször
azt feltételezzük, hogy a megkérdezettek tényleges
jövedelme és a nyeremény-/veszteségösszegek
közvetlenül mint döntési paraméterek jelennek
meg a vizsgált döntési helyzetben. Ezzel szemben az
olyan változókat, mint a nemi hovatartozás, az életkor,
az iskolai végzettség vagy a megkérdezettek foglalkozási/munkaerõ-piaci
státusa, a preferenciák formálódására
ható demográfiai és társadalmi tényezõknek
tekintjük.
Adatok és módszerek
Ebben az alfejezetben áttekintjük az empirikus vizsgálat alapvetõ feltevéseit és keretfeltételeit. Elõbb az operacionalizálásról, majd a mintákról és a kérdezés körülményeirõl lesz szó.
Operacionalizálás. A kockázatkerülésre vonatkozó attitûdöt az irodalomban szokásosan alkalmazott kérdésblokkal igyekeztünk feltérképezni. A megkérdezetteknek két lehetõség közül - egy biztosan realizálható fix összegû "ajándék" és egy kockázatos kimenetelû szerencsejáték között - kellett választaniuk. A játékban 50 százalék valószínûséggel nyerhették a fix összeg kétszeresét, de - természetesen - ugyanakkora volt a valószínûsége annak is, hogy nem nyernek semmit. Egymás után három kérdés hangzott el. A kérdések szerkezete megegyezett, a nyeremények összege viszont emelkedett. A kérdésblokk szerkezetét formálisan a 2. táblázat mutatja.
2. táblázat
A kérdõívben szereplõ kérdésblokk
formális szerkezete
|
|
|
|||
|
|
(forint) |
(százalék) |
(forint) |
(százalék) |
|
|
1000
|
100
|
2000
0 |
50 |
|
|
100 000
|
100
|
200 000
0 |
50 |
|
|
1 000 000
|
100
|
2 000 000
0 |
50 |
Adatok. Az adatok forrását a TÁRKI által 1996 októberében és 1997 januárjában folytatott vizsgálatok adják. Az itt vizsgált kérdésblokk mindkét alkalommal szerepelt, pontosan ugyanabban a megfogalmazásban. Mindkét vizsgálat 1500 fõs, a felnõtt, 18 év feletti lakosságot reprezentáló, többlépcsõs rétegzettséggel készített valószínûségi mintákon zajlott, személyes megkérdezéssel. Az egyes minták illeszkedésének vizsgálata súlyozást nem tett szükségessé, azok az alapsokaságot a legfontosabb társadalmi és demográfiai dimenziók mentén kellõen pontosan reprezentálták.
Tekintettel arra, hogy mindkét vizsgálat azonos megfogalmazással tartalmazta a kulcskérdéseket, továbbá a két vizsgálat között viszonylag rövid idõ telt el, valamint külön-külön mindegyik minta kielégítõen illeszkedik az alapsokasághoz, úgy ítéltük meg, hogy lehetséges a két minta összevonása. Erre elsõsorban azért volt szükség, hogy nagyobb esetszámokkal rendelkezzünk, és ennek révén részletesebb elemzésekre nyíljon lehetõségünk. Összességében tehát 3000 fõs mintát elemzünk. Ekkora minta esetében kapott adatok már 95 százalékos valószínûséggel legfeljebb 1,5-2 százalékkal térnek el attól, amit akkor kaptunk volna, ha a teljes sokaságot megkérdeztük volna.
Kérdõív-kontextus. Az adatok egy olyan kérdõívbõl
származnak, amelynek kontextusát alapvetõen a nyugdíjreformmal
kapcsolatos kérdésblokkok, valamint a kormányzat szerepével
és a munkával kapcsolatos attitûdökkel foglalkozó
ISSP-modulok7 határozták
meg. Ezen túl mindegyik kérdõív végén
részletes politikai blokk szerepelt. Az általunk vizsgált
kérdésblokkot azonban mindkét esetben néhány
személyes, elsõsorban a munkaerõ-piaci státussal
kapcsolatos kérdés, valamint a két esetben egymással
csaknem teljesen megegyezõ, a nyugdíjrendszerrel kapcsolatos
ismereteket és a nyugdíjreformmal kapcsolatos preferenciákat
vizsgáló kérdés kísérte.
Hipotézisek
A konkrét hipotézisek megfogalmazása elõtt vissza kell térnünk az analitikus modell szerkezetéhez. A modell független változója az egyének kockázattal szembeni attitûdje. Elõször tehát azt kell operacionalizálnunk, kit is tekintünk kockázatkerülõnek, kockázatsemlegesnek és kockázatkedvelõnek. A kérdõívben feltett kérdés így hangzott: "Mit választanának: a biztos nyereményt vagy a szerencsejátékot?" Adott feltételek mellett, ha a várhatóhasznosság-paradigmát fogadjuk el kiindulásnak, akkor azt kell mondanunk, hogy a két választási lehetõség (a biztos ajándék és a kockázatos szerencsejáték) várható értéke az adott valószínûségek mellett azonos: 1000, 100 000 és 1 000 000 forint az egymást követõ fordulókban. Ebben az esetben, ha lett volna olyan válaszlehetõség, hogy a megkérdezettek egyszerûen közömbösnek mutatkozzanak, a várhatóhasznosság-paradigma szerint a kockázatsemleges döntéshozóknak mindhárom esetben a közömbösséget kellett volna választaniuk. Ilyen válaszlehetõség azonban nem volt. Hipotézist tehát elsõsorban arra tudunk megfogalmazni, hogy milyen mértékben fog egymástól eltérni az egyik vagy a másik lehetõséget választók aránya. Ha mindenki közömbös lenne, és valamilyen kényszerhelyzetben véletlenszerûen választanák az egyik vagy a másik lehetõséget, akkor összességében azt feltételezhetnénk, hogy a megkérdezettek fele fogja a biztos nyereményt és fele a kockázatos, ám nagyobb nyereményt választani. A standard döntéselméleti irodalom egyértelmûen azt sugallja azonban, hogy efféle helyzetekben a kockázattal szembeni idegenkedés a tipikus attitûd. Esetünkben ez - a kockázatkerülés korábban adott definíciójával összhangban - azt jelenti, hogy akik idegenkednek a kockázattól, azok azonos várható értékek esetén elõnyben részesítik a biztos nyereményt a kockázatoshoz képest. Elsõ hipotézisünk szerint tehát:
1. hipotézis (H1.): kockázatos döntési helyzetekben a nyereségek tartományában a kockázatkerülés (kockázattal szembeni idegenkedés) a tipikus kockázattal szembeni attitûd.
Ezt a hipotézist a fenti esetben akkor tekinthetjük elfogadottnak, ha a biztos nyereményt választók száma a mintában szignifikánsan meghaladja azoknak a számát, akik a kockázatos nyeremény mellett vannak. A hipotézis egyfelõl világosan levezethetõ az elméleti modellbõl, másrészt ezt korábbi - többnyire kísérleti - vizsgálatok egész sora támasztja alá8.
A döntési helyzetet árnyalhatjuk, ha végiggondoljuk, hogy a megkérdezettek valójában a következõképpen okoskodhatnak: "Ha válaszolok a kérdésre, már kapok ezer (százezer, egymillió) forintot. Ha ezek után mindezt kockára teszem, két eset lehetséges: vagy nyerek kétszer annyit, vagy elvesztem azt is, amit eddig kaptam." Efféle okoskodás esetén valójában nem is az az érdekes, hogy van kockázatkerülésre utaló hajlam, hanem az, hogy a biztos és ingyenes ajándék ellenére vannak olyanok, akik ezt - dupla vagy semmi alapon - kockára tennék. Eddig nem mondtunk mást, mint hogy a fent megfogalmazott hipotézis nem kizárólagos. Másképpen: a kockázattal szembeni idegenkedés a tipikus attitûd a nyereségek tartományában, mégis léteznek olyan döntéshozók, akik a kockázatkedvelés jeleit mutatják ebben a tartományban.9 Ezt akár az elsõ hipotézis alhipotézisének is tekinthetjük:
H1.a) Kockázatos döntési helyzetekben a nyereségek tartományában a tipikus kockázatkerülési attitûd mellett elõfordul a kockázatkedvelési attitûd.
Ez a részhipotézis csak annyit mond, hogy vannak olyanok, akik adott körülmények között kockáztatnak. Elméleti szempontból ennek az empirikus részhipotézisnek elsõsorban az a jelentõsége, hogy explicitté teszi azt, hogy a valóságban többféle kockázattal szembeni attitûd létezik ugyanabban a tartományban, s így feloldható az ökonómiai közelítésmód szokásos feltevése, miszerint a gazdasági szereplõk ugyanolyan preferenciákkal (haszonfüggvényekkel) rendelkeznek10.
A továbbiakban lényegében azt vizsgáljuk, hogy milyen tényezõktõl függ a H1., illetve a H1.a hipotézisekben specifikált kockázattal szembeni attitûd. Kezdjük a legkézenfekvõbb tényezõvel, a "nyereség" nagyságával. Az általunk meghatározott helyzetben minden döntés két összegrõl szól. Az egyik a biztos 1000 forint, a másik pedig a kockázatos 2000 forint. Ebbõl kiindulva, két irányban fogalmazhatunk meg hipotéziseket. Egyfelõl, ha adottnak vesszük a biztos nyereség nagyságát, azzal a feltételezéssel élhetünk, hogy a kockázatos nyeremény várható értékének növekedése nagyobb kockázatvállalási hajlandóságot hoz magával. Másfelõl: adottnak véve a kockázatos nyereményt, feltételezhetjük, hogy a nagyobb biztos nyeremény kisebb kockázatvállalási hajlandósággal jár együtt.
A mi esetünkben - a kérdõíves adatfelvétel adta keretek között - olyan hipotézis elõterjesztésére van mód, amely szimultán módon fogalmazza meg a biztos és a kockázatos nyeremény függvényében a kockázatvállalási hajlandóság alakulását. Ezt - a szabatosság követelményeit szem elõtt tartva - az egyes "játszmák" várható értékeinek terminusaiban a következõképpen fogalmazhatjuk meg:
2. hipotézis (H2.): minél nagyobb az egyes döntési helyzetekben a két választási lehetõség várható értéke, annál kisebb lesz a kockázatvállalási hajlandóság.
Indoklásképpen ismét visszatérhetünk a H1.a megfogalmazása elõtt kifejtett okoskodáshoz: Minél nagyobb a biztos nyeremény, annál kisebb a kockázatvállalási hajlandóság. Ez, úgy véljük, hatásában felülmúlja a kockázatos nyeremények nagyságának emelkedésébõl fakadó hatást.
A következõ lépésben a megkérdezettek egyes társadalmi-demográfiai jellemzõi és kockázattal szembeni attitûdje közti összefüggésekre vonatkozóan állítunk fel hipotéziseket. Nyilvánvaló, hogy ebben megkülönböztetett jelentõsége van a megkérdezettek jövedelmének. A jövedelemnek magyarázó változóként való figyelembe vételekor kiindulhatunk a pénz csökkenõ határhasznából. Hétköznapi nyelven megfogalmazva ez azt jelenti, hogy adott körülmények között nagyobb jövedelem esetén a pótlólagos összegek relatíve kisebb hasznot jelentenek a jövedelmek tulajdonosainak. Különösen így lenne ez akkor, ha a pénz megszerzésének költségeit (a szükséges munkabefektetéseket) is tekintetbe vennénk. Ha ez a feltételezés helytálló, akkor megfogalmazhatjuk a következõ hipotézist:
3. hipotézis (H3.): az egyéb körülményeket változatlannak tekintve, a jövedelmek növekedésével növekszik a kockázatvállalási hajlandóság.
Ez a hipotézis nem fogalmaz meg egyebet, mint azt, hogy az egyéni jövedelmek növekedésével egyre kisebb a jelentõsége annak a veszteségnek, amit a biztos nyeremény elvesztése idézhet elõ akkor, ha vállalja a szerencsejátékot11.
A kockázattal szembeni attitûd meghatározásának további társadalmi-demográfiai jellemzõit illetõ hipotéziseinkre inkább intuitív, s kevésbé feszes indoklást tudunk adni. Három ilyen hipotézist fogalmazunk meg. Mindegyikrõl azt gondoljuk, hogy különbözõ áttételeken keresztül hatnak a pénzzel, pénzkezeléssel és a kockázattal kapcsolatos attitûdökre, részben összetételi hatásokon keresztül, részben pedig önállóan is.
4. hipotézis (H4.): az iskolai végzettség növekedésével növekszik a kockázatvállalási hajlandóság.
5. hipotézis (H5.): az életkor növekedésével csökken a kockázatvállalási hajlandóság.
6. hipotézis (H6.): a férfiak kockázatvállalási hajlandósága nagyobb a nõk kockázatvállalási hajlandóságánál12.
A tanulmány második felében fogunk amellett érvelni, hogy az efféle kísérleti helyzetek általában eléggé "steril" eredményeket adnak. A rendelkezésre álló szûkös adatok segítségével a késõbbiekben érdemes lehet megvizsgálni, hogy az ilyen, "laboratóriumi módon" definiált kockázattal szembeni attitûd milyen empirikus összefüggéseket mutat a tényleges viselkedéssel (például azzal, hogy rendelkezik-e biztosítással az illetõ, vagy azzal, hogy miképpen készül fel idõs korára). A kockázatvállalási hajlandóság meghatározói között minden bizonnyal kitüntetett szerepe lesz az efféle változók között a megkérdezettek foglalkozásának is. Úgy véljük, hogy megfogalmazhatjuk a következõ hipotézist ezzel kapcsolatban:
7. hipotézis (H7.): a foglalkozási státus önmagában (az összetételi hatásokon túl) is hatást gyakorol a kockázatvállalási hajlandóságra.
Pontosabban, úgy véljük, hogy a foglalkozásnak
van egy olyan dimenziója, amelyet semmiképpen nem magyarázhatnak
egyéb összetételi hatások (például
iskolai végzettség, nemi hovatartozás, életkor
és jövedelem). Ez pedig nem más, mint a munka önálló,
független jellege.
Elemzés
Kockáztatás: az alapadatok leírása
Kockáztatás és a "tétek" nagysága. Elemzésünket annak vizsgálatával kezdjük, hogy az egyes mintákban mekkora azoknak az aránya, akik a vizsgált döntési helyzetben a szerencsejáték mellett döntöttek! Megoszlásukat a 3. táblázat mutatja.
3. táblázat
A szerencsejátékot választók aránya
az összes megkérdezett százalékában
| Tét |
|
|
|
|
|
|
||
| Kicsi (ezer forint) |
|
|
|
| Közepes (százezer forint) |
|
|
|
| Nagy (egymillió forint) |
|
|
|
A két minta eredményeinek összehasonlításából elõször is szembeötlõ, hogy mennyire hasonló eredményeket találtunk. Az egyes tétek esetén a szerencsejátékot választók aránya az adott minták nagyságát is figyelembe véve (ne felejtsük el, hogy 1500 fõs minták esetén a becslések hibahatára nagyobb, mintegy ± 2,5-3 százalék) nem különbözik lényegesen egymástól.13
De nem ez az egyetlen következtetés. Összességében a szerencsejátékot kis tét esetén 34 százalék, közepes tét esetén 17 százalék, nagy tét esetén pedig 7,6 százalék választotta. Láthatjuk tehát, hogy a szerencsejátékot választók aránya még a legkisebb tét esetében is körülbelül a teljes népesség egyharmada körül van. A többiek 50 százalékot meghaladó aránya (legalábbis indirekt módon) a kockázattal szembeni idegenkedés jelenlétét mutatja (vö. H1. hipotézis). Az is tény azonban, hogy még a legnagyobb tét esetében is körülbelül minden tizenkettedik-tizenharmadik ember kockázatvállaló (vö. H1.a hipotézis).
Ha egy lépéssel továbbmegyünk, megvizsgálhatjuk, hogyan döntöttek a megkérdezettek az egymást követõ fordulókban. Ezt mutatja a 4. táblázat. A táblázatban azt tüntettük fel, hogy az egyes döntési szinteken (ezer, százezer és egymillió forintos téteknél) mekkora a biztos nyereményt és a szerencsejátékot választók aránya. Az egyes cellákban a két opciót választók megoszlása szerepel. Dõlt számmal mindig azoknak az arányát tüntettük fel, akik a játékot választották, vastagon pedig azokét szedtük, akik a biztos pénz mellett voltak. A következõ cella mindig az adott döntést hozók további megoszlását mutatja a döntési folyamat következõ fázisaiban. Például a bal felsõ cella adata azt mutatja, hogy az összes megkérdezett 66,2 százaléka választotta a biztos pénzt az elsõ fordulóban. A tét emelése után 97,5 százalék továbbra is a biztos pénzt választja, és alig 1,1 százalék dönt inkább a szerencsejáték mellett a legnagyobb tét esetében is.
Az adatok vizsgálatából a következõ rajzolódik ki. Akik a kérdésblokk elején a kis pénz esetén a biztos "ajándékot" választották, azok a következõ fordulókban is megmaradtak a biztos pénzek mellett. Akik viszont az elsõ fordulóban kockára tették a biztos ezer forintot, azok a tétek emelése esetén egyre kisebb mértékben döntenek már így. Az elsõ fordulóban szerencsejátékot választók 54 százaléka a második fordulóban már a biztos pénzt választja és elsöprõ többségben (97%) ugyanígy tesz a harmadik fordulóban is.
Mindezek az eredmények a H2. hipotézist igazolják. Arról van ugyanis szó, hogy határozott tendencia mutatkozik arra, hogy a kockára tehetõ tét nagyságával együtt csökken azoknak az aránya, akik a szerencsejáték mellett vannak.
4. táblázat
Továbblépési esélyek a kérdezés
egyes fázisaiban: az egymást követõ fordulókban
a nagyobb tétek esetén a szerencsejátékot (dõlt
szám) és a biztos pénzt (vastag szám) választók
százalékos megoszlása
|
(ezer forint) |
(százezer forint) |
(egymillió forint) |
|
|
||
|
|
||
|
|
|
|
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
|
|
|
|
||
|
|
Kockáztatás és a jövedelem. A következõ lépés annak vizsgálata, hogy milyen összefüggés mutatkozik a jövedelmek és a kockázattal szembeni attitûdök között. Ennek részletesebb vizsgálatához rövid kitérõt kell tenni a jövedelmek lehetséges definíciójáról. Adatfelvételünk három különbözõ jövedelemtípus definícióját és hatásainak empirikus vizsgálatát teszi lehetõvé. Rendelkezésünkre áll a megkérdezettek havi személyes nettó jövedelme. Ezt a jövedelemfajtát tekintjük a kiindulópontnak, amely az adott egyének erõforrásait jelzi. Világos ugyanakkor, hogy azokat a rendelkezésre álló jövedelmeket, amelyeket a vizsgált szituációban döntési argumentumként szerepelhetnek, a személyes jövedelmeken kívül a háztartás többi tagjának jövedelme is befolyásolhatja. A második lépcsõben ezért a háztartás (havi, nettó) összes jövedelem fogalmát használjuk. Végezetül, harmadik jövedelemfogalomként a háztartás egy fõre jutó jövedelmeit tekintjük magyarázó változónak. Ez a jövedelemkoncepció a háztartási szükségletek tekintetbevételével, feltételezésünk szerint, alkalmasabb lehet a tényleges döntési helyzetek eredményeinek elõre jelzésére.
Akármilyen jövedelemfogalmat használjunk is, mindhárom fordulóban szignifikánsan eltér egymástól a biztos pénzt választók és a játék mellett döntõk átlagos jövedelme. Úgy látszik, a két csoport jövedelemének különbsége a második fordulóban a legnagyobb: az átlagok itt különböznek a legjobban egymástól. Minden egyes esetben igaz azonban az, hogy a biztos pénzt választók átlagos jövedelme lényeges mértékben alacsonyabb a kockáztatókénál. A legnagyobb eltéréseket a háztartáslétszámmal nem korrigált jövedelmek esetében látunk, a középsõ fordulóban a kockáztatók és a biztos nyereményeket elõnyben részesítõk közötti jövedelemkülönbség több mint 35 százalékos (5. táblázat). Általában úgy tûnik, hogy a nagyobb tétek esetében kisebb az egyes csoportok közti jövedelemkülönbség: valószínûleg ebben az esetben kisebb a jövedelmek hatása a kockázatvállalási hajlandóságra.
5. táblázat
A szerencsejátékot és a biztos nyereményt
választók átlagjövedelme a különbözõ
jövedelemfogalmak mellett a tétek különbözõ
szintjein
|
|
|
|
|
tika |
ciaszint |
|
|
|
||||||
| Biztos 1000 forint |
42 441
|
27 304
|
1663
|
60,73
|
0,0000
|
|
| Kockáztatott 2000 forint |
52 898
|
37 909
|
796
|
|
||
| Biztos 100 000 forint |
43 280
|
26 350
|
2067
|
84,88
|
0,0000
|
|
| Kockáztatott 200 000 forint |
58 849
|
48 145
|
400
|
|
||
| Biztos 1 000 000 forint |
45 385
|
30 994
|
2295
|
5,81
|
0,0160
|
|
| Kockáztatott 2 000 000 forint |
51 359
|
36 728
|
173
|
|
||
| Összesen |
45 804
|
31 459
|
2468
|
|
||
|
|
||||||
| Biztos 1000 forint |
16 030
|
9 826
|
1663
|
14,77
|
0,0001
|
|
| Kockáztatott 2000 forint |
18 000
|
15 347
|
796
|
|
||
| Biztos 100 000 forint |
15 979
|
9 072
|
2067
|
45,02
|
0,0000
|
|
| Kockáztatott 200 000 forint |
20 305
|
20 837
|
400
|
|
||
| Biztos 1 000 000 forint |
16 447
|
11 426
|
2295
|
11,94
|
0,0006
|
|
| Kockáztatott 2 000 000 forint |
19 687
|
16 920
|
173
|
|
||
| Összesen |
16 674
|
11 918
|
2468
|
|
||
|
|
||||||
| Biztos 1000 forint |
22 569
|
16 102
|
1542
|
20,57
|
0,0000
|
|
| Kockáztatott 2000 forint |
26 553
|
25 086
|
713
|
|
||
| Biztos 100 000 forint |
22 673
|
15 295
|
1910
|
43,42
|
0,0000
|
|
| Kockáztatott 200 000 forint |
30 018
|
33 367
|
354
|
|
||
| Biztos 1 000 000 forint |
23 628
|
19 278
|
2109
|
2,74
|
0,0979
|
|
| Kockáztatott 2 000 000 forint |
26 308
|
21 555
|
155
|
|
||
| Összesen |
23 812
|
19 449
|
2264
|
|
||
A szerencsejáték választása és a jövedelem közötti összefüggés megvilágítására megnéztük részletesebben, hogyan alakul a játék választásának valószínûsége a különbözõ jövedelmi szinteken. Ennek érdekében a következõ megválaszolásra váró kérdés a jövedelmi szintek meghatározásának módszere volt. Erre - több lehetõség megfontolása után az egyszerûség kedvéért - azt a módszert alkalmaztuk, hogy az egyes megkérdezetteket aszerint soroltuk csoportokba, hogy adott jövedelmeik alapján milyen távolságra vannak a medián jövedelemtõl. E távolság alapján soroltuk õket osztályközökbe és az így kialakított rangsorok szerint határoztuk meg a jövedelmi szinteket.14 A kockázattal szembeni attitûdöt az ily módon definiált jövedelmi kategóriákban a Függelék F1. táblázata mutatja.
Elsõ látásra úgy tûnik, mindegyik jövedelemfogalom használata esetén megfogalmazhatjuk a következõ kísérleti megállapítást: a magasabb jövedelemcsoportokban nagyobb a szerencsejátékot választók aránya. Ugyanakkor azt is látni kell, hogy az összefüggés nem látszik egyértelmûen lineárisnak. A jövedelemegyenlõtlenségekkel foglalkozó szociológiai szakirodalomban gyakran használják relatív szegénységi küszöbként a medián jövedelmek ötven százalékát. A mi esetünkben - úgy tûnik - szintén van ennél a pontnál egyfajta törése a kockázatvállalási hajlandóságnak. A kockázatvállalásra hajlandóságot mutató megkérdezettek aránya a jövedelmeknek e szintjéig nem változik, vagy csökken, és ezután indul növekedésnek a jövedelmek növekedésével. Ez a jellemzõ különösképpen markánsnak mutatkozik a háztartás egy fõre jutó jövedelme tekintetében.
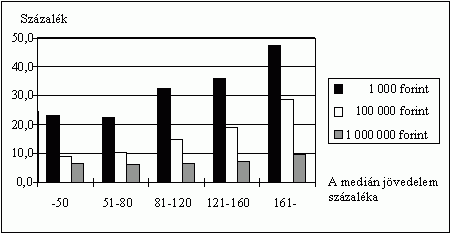
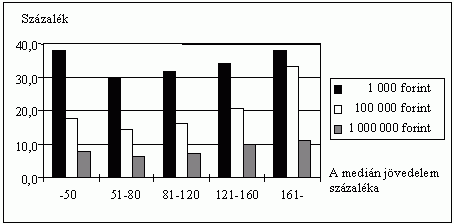
Ezek az eredmények tehát, úgy tûnik, a H3. hipotézis mellett szólnak, azzal a megszorítással, hogy a jövedelmek és a kockázatvállalási hajlandóság között enyhe J-alakú összefüggés mutatkozik. A szerencsejátékot választók arányát a különbözõ tétek mellett a jövedelmek különbözõ szintjein mutatja a 3., 4., és 5. ábra. Ezek a következõ megállapításokat illusztrálják:
- a jövedelmek növekedésével (a fent említett enyhe J mintát követve) növekszik a szerencsejátékot választók aránya;
- a legnagyobb tét esetén a szerencsejátékot választók aránya kisebb mértékben nõ a jövedelmek növekedésével, mint a legkisebb tét esetében.
A fentiek segítenek bennünket annak értelmezésében is, amit korábban a kockázatkedvelés és a "tétek" nagysága közötti kapcsolatról mondottunk. Láthatjuk ugyanis, hogy a kockázatvállalási hajlandóság egyfelõl csökken a kockáztatható "ajándék" növekedésével, másfelõl növekszik a jövedelmek növekedésével. A tényleges kockáztatási hajlandóságot tehát e két tényezõ együttes hatása határozhatja meg.
3. ábra
A játékot választók aránya különbözõ
tétek mellett a háztartás medián jövedelem
különbözõ szintjein, százalék
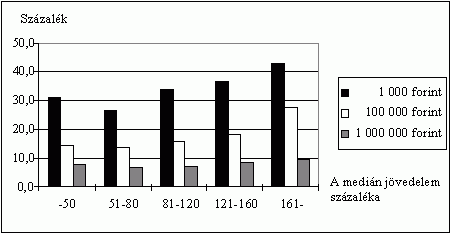
4. ábra
A játékot választók aránya különbözõ
tétek mellett a háztartás egy fõre jutó
medián jövedelem különbözõ szintjein,
százalék
5. ábra
A játékot választók aránya különbözõ
tétek mellett a személyes medián jövedelem különbözõ
szintjein, százalék
Kockáztatás és az egyéb társadalmi-demográfiai jellemzõk. A kockázattal szembeni attitûd társadalmi tényezõire vonatkozó hipotéziseink mindenekelõtt az iskolai végzettség (H4. hipotézis), az életkor (H5. hipotézis) és a nemi hovatartozás (H6. hipotézis) meghatározó szerepére vonatkoztak.
Iskolai végzettség. A 6. táblázatban bemutatott adatok szerint mindhárom szinten eltér egymástól a kockázatvállalók és a kockázatkerülõk által elvégzett iskolai osztályok átlagos száma. A legalacsonyabb és a középsõ tét szintjén ez az eltérés valamivel több, mint egy év, a legmagasabb tét esetében pedig mintegy 0,7 iskolai év.
6. táblázat
A szerencsejátékot és a biztos nyereményt
választók által elvégzett iskolai osztályok
átlagos száma a tétek különbözõ
szintjein
|
|
|
|
|
tisztika |
ciaszint |
|
|
| Biztos 1000 forint |
|
|
|
|
|
| Kockáztatott
2000 forint |
11,4 |
2,7 |
982 |
||
|
|
| Biztos 100 000 forint |
|
|
|
|
|
| Kockáztatott
200 000 forint |
11,6 |
2,7 |
503 |
||
|
|
| Biztos 1 000 000 forint |
10,6 |
3,0 |
2691 |
10,32 |
0,0013 |
| Kockáztatott
2 000 000 forint |
11,3 |
2,7 |
220 |
||
Ennél többet tudhatunk meg az iskolai végzettség és a kockázatvállalási hajlandóság kapcsolatáról, ha a különbözõ iskolai végzettségi szinteken mutatjuk be a kockázatvállalók arányát. Az ezt mutató F3. táblázat (lásd a Függelékben) szerint a kockázatvállalási hajlandóság magasabb a befejezett középiskolát végzettek között, mint az alacsonyabb iskolai végzettségûek körében. Ugyanakkor a felsõfokú végzettséggel rendelkezõk kockázatvállalási hajlandósága már nem tér el statisztikai értelemben a középiskolát végzettekétõl. Ezt a tényt érdemes lenne tovább vizsgálni, és bizonyos fokig vissza is térünk rá a késõbbiekben. Ezek az eredmények tehát csak részben támasztják alá H4. hipotézisünket.
Életkor. Rátérve az életkor és a kockázatvállalási hajlandóság közötti összefüggésekre, az elemzést most is a magyarázó változó átlagának és szórásának vizsgálatával kezdjük. A kockáztatók átlagos életkora mindhárom tét esetében lényegesen alacsonyabb azokénál, akik inkább a biztos pénzt választották. Itt most azt láthatjuk, hogy az igazán nagy különbségek a középsõ szinten alakulnak ki: itt a két csoport átlagos életkora több mint 11 évvel különbözik egymástól (7. táblázat).
7. táblázat
A szerencsejátékot és a biztos nyereményt
választók átlagos életkora a tétek különbözõ
szintjein
|
|
|
|
|
tisztika |
|
|
|
|||||
| Biztos 1000 forint |
|
|
|
|
|
| Kockáztatott 2000 forint |
|
|
|
|
|
|
|
|||||
| Biztos 100 000 forint |
|
|
|
|
|
| Kockáztatott 200 000 forint |
|
|
|
|
|
|
|
|||||
| Biztos 1 000 000 forint |
|
|
|
|
|
| Kockáztatott 2 000 000 forint |
|
|
|
|
|
A kockázatvállalási hajlandóságot az egyes életkori csoportokban bemutató adatokból az derül ki, hogy a megkérdezettek életkora egyértelmûbb hatást gyakorol a kockázatvállalási hajlandóságra, mint amint azt az iskolai végzettség esetében láttuk: minél magasabb az életkora valakinek, annál alacsonyabb a kockázatvállalási hajlandósága (F4. táblázat). Ez a hatás a középsõ tét esetében tûnik a legmarkánsabbnak, de mind a három szinten jelen van valamilyen mértékben. Ez amellett szól, hogy H5. hipotézisünk nem volt megalapozatlan.
Életkor és iskolai végzettség együttes hatása. A F5. táblázat szerint (amelyben a szerencsejátékot választók arányát együttesen vizsgáljuk az egyes életkori és iskolai végzettségi csoportokban) az életkornak és az iskolai végzettségnek egyaránt fontos szerepe lehet a kockázatvállalási hajlandóság meghatározásában. A különbözõ iskolai végzettségi csoportokon belül mindhárom tét esetében csökken a kockázatvállalás valószínûsége az életkor emelkedésével.15
Nemi hovatartozás. H6. hipotézisünk szerint a férfiak kockázatvállalási hajlandósága magasabb, mint a nõké. Ezt elõször egyszerû kereszttábla segítségével teszteljük. Ebbõl elsõ megközelítésben úgy tûnik, mintha igazolást nyerne szóban forgó hipotézisünk: a férfiak kockázatvállalási hajlandósága mindhárom tét esetében szignifikánsan nagyobbnak tûnik, mint a nõké (8. táblázat). Elõrebocsátjuk azonban, hogy e mögött lényeges összetételi hatások húzódhatnak meg: a férfiak korszerkezete, iskolai végzettség szerinti megoszlása és jövedelmi helyzete egyaránt lényegesen eltér a nõkétõl. Ezért erõsebb megállapításokat a nemek szerinti hatásokra vonatkozóan csak akkor tehetünk, ha majd a késõbbiekben megkíséreljük kiszûrni az efféle összetételi hatásokat.
8. táblázat
A kockázatvállalók (szerencsejátékot
választók) aránya a férfiak és a nõk
között, a tétek különbözõ szintjein
|
|
|
|
||
|
|
|
|
|
|
| Nõ |
|
|
|
|
| Férfi |
|
|
|
|
| c 2 |
|
|
|
|
| Szignifikanciaszint |
|
|
|
|
Foglalkozás. Kiinduló H7. hipotézisünk
szerint a foglalkozás szintén hatással van a kockázattal
szembeni attitûdre. A hipotézis ellenõrzéséhez
vessünk egy pillantást az F6. táblázatra,
amelyik az egyes foglalkozási csoportokon16
belül mutatja a kockázatvállalók arányát.
A legalacsonyabb tét esetében az értelmiségiek,
az alsó szintû vezetõk, az önállóak,
valamint a munkahellyel még életükben nem rendelkezõk
kockázatvállalási hajlandósága haladja
meg jelentõsebb mértékben az átlagot. A középsõ
tét esetében a játékot választó
önállóak aránya lényegesen meghaladja,
a mezõgazdasági fizikai foglalkozásúaké
pedig lényegesen alulmúlja az átlagot. A legmagasabb
tét esetében lényegében ugyanez a helyzet.
A foglalkozásicsoport-hovatartozásnak a kockázatvállalási
hajlandóságra gyakorolt hatását még
alaposabban kell elemeznünk a késõbbiekben. Mi most
az egyszerûség kedvéért a további elemzés
céljára a foglalkozási csoportok lehetséges
összevonásával próbálkozunk: külön
fogjuk vizsgálni az önálló foglalkozásúak
attitûdjeit és az összes többi foglalkozási
csoporthoz tartozók attitûdjeit.
Többváltozós elemzés
Az eddigiekben többször utaltunk rá, könnyen lehetséges, hogy összetételi hatások húzódnak meg egyes eredmények mögött. Megeshet például, hogy a férfiak és a nõk eltérõ kockázatvállalási hajlandósága nem valamiféle "genetikai" vagy szocializációs okokkal magyarázható, hanem eltérõ jövedelmi, képzettségi vagy éppen életkori szerkezettel. De hasonlóképpen elõfordulhat, hogy az iskolai végzettség szerinti eltérések "eltûnnek" akkor, ha a függõ változónk eloszlását valami más független változóra kontrolláljuk. Ezért most megvizsgáljuk, hogy a tanulmányunk elején specifikált magyarázó változóink közül melyek azok, amelyek szignifikáns mértékben hatnak a kockázatvállalási hajlandóságra.
Erre a célra a logisztikus regressziós eljárás
tûnik a leginkább alkalmasnak. A szóban forgó
módszer azokban az esetekben alkalmazható, amikor a független
változónk kétértékû (dummy),
a függõ változók pedig lehetnek egyaránt
kategorikusak, ordinálisak és intervallumskálán
mérhetõk. Ennek az eljárásnak továbbá
nincsenek olyan szigorú feltevései a vizsgált változók
eloszlására vonatkozóan, mint más eljárásoknak.
A logisztikus regresszió lényege, hogy közvetlenül
próbáljuk megbecsülni adott esemény elõfordulásának
valószínûségét. Ha több magyarázó
változónk van, akkor adott esemény bekövetkezési
valószínûségét a következõ
egyenlettel becsülhetjük:
Prob(esemény)=1/(1+e-z),
Z=B0+B1X1+B2X2+ ... BkXk,
Modellünkben a magyarázni kívánt változó a kockázattal szembeni attitûd, amit a különbözõ szinteken bemutatott szerencsejátékokban való részvétellel mérünk (JÁTÉK1, JÁTÉK2 és JÁTÉK3, részvétel = 1, részvételtõl való tartózkodás = 0).
Magyarázó változóinkat a következõképpen
definiáltuk:
KOR = a megkérdezettek életkora hat kohorszba csoportosítva (-29, 30-39, 40-49, 50-59, 60-69 és 70- évesek megkülönböztetésével),
ISKOLAi= a megkérdezettek iskolai végzettsége három kategóriába sorolva (i = 1: legfeljebb alapfok, i = 2 középfok és i = 3 felsõfok),
NEM = a megkérdezettek neme (0= nõ, 1= férfi),
ONALLO = a megkérdezettek foglalkozási státusa
(kétértékû változó, 0= nem önálló,
1= önálló).
prob (JÁTÉKi) = 1/(1+e-z),
Z=B0+B1*LG10JOV+B2*KOR+ B3*ISKOLA3+B4*NEM+B5*ONALLO.
9. táblázat
A regressziós modell eredményei a három különbözõ
tét esetén (a modellek valamennyi magyarázó
változó együttes figyelembe vételével
készültek)
|
|
ható |
hiba |
|
ciaszint |
|
exp(B) |
|
|
||||||
| LG10JOV |
|
|
|
|
|
|
| KOR |
|
|
|
|
|
|
| ISKOLA3 |
|
|
|
|
|
|
| NEM |
|
|
|
|
|
|
| ONALLO |
|
|
|
|
|
|
| Konstans |
|
|
|
|
|
|
|
|
||||||
| LG10JOV |
|
|
|
|
|
|
| KOR |
|
|
|
|
|
|
| ISKOLA3 |
|
|
|
|
|
|
| NEM |
|
|
|
|
|
|
| ONALLO |
|
|
|
|
|
|
| JATEK1 |
|
|
|
|
|
|
| Konstans |
|
|
|
|
|
|
|
|
||||||
| LG10JOV |
|
|
|
|
|
|
| KOR |
|
|
|
|
|
|
| ISKOLA3 |
|
|
|
|
|
|
| NEM |
|
|
|
|
|
|
| ONALLO |
|
|
|
|
|
|
| JATEK1 |
|
|
|
|
|
|
| JATEK2 |
|
|
|
|
|
|
| Konstans |
|
|
|
|
|
|
A játék elsõ fordulójában a Wald-statisztika 5 százalékos szignifikanciaszintje mellett a jövedelem (LG10JOV) és az iskolai végzettség (ISKOLA) gyakorol pozitív hatást a kockázatvállalási hajlandóságra (JÁTÉK1). Ugyanezen a szinten szignifikáns, ámde negatív a KOR magyarázó változó hatása. A NEM hatása az eddigieknél lényegesen gyengébb, az ONALLO változó pedig egyáltalán nem gyakorol hatást. A jövedelemhez tartozó esélyráta értéke 2,4, ami azt jelenti, hogy a jövedelem logaritmusának egy egységnyi (tehát magának a jövedelemnek a tízszeresére történõ) növekedése esetén a játék választásának esélyhányadosa a 2,4-szeresére nõ. Vagyis: ha adott X személynek havi 100 ezer forint jövedelme van, és a 10 ezer forintnyi jövedelem esetén (egyéb tényezõk változatlansága mellett) a játék választásának valószínûsége 30 százalék (esélyhányados = 3/7 = 0,42) volt, akkor X esetében a játékválasztási valószínûséget körülbelül 50-51 százalékra becsülhetjük (esélyhányados = 3x2,4/7 = 1,03).
A középsõ tét esetében valamennyi magyarázó változó szignifikáns hatást gyakorol, az iskolai végzettség és a nem p<0,1 szinten, a többi változó pedig p<0,05 szinten. Meg kell jegyeznünk, hogy a KOR hatása itt az elõbbinél lényegesen gyengébb, erõteljesebb pozitív hatást gyakorló viszont a kockázatvállalási hajlandóságra az önálló foglalkoztatotti státus (ONALLO) és az a tény, ha valaki az elõzõ fordulóban is részt vett a játékban.
A legnagyobb tét esetében mindössze két magyarázó változónknak van szignifikáns hatása a kockázatvállalási hajlandóságra: a megkérdezettek háztartásának jövedelme (LG10JOV) és ennél lényegesen nagyobb mértékben a második fordulóban való részvétel ténye (JATEK2). Érdemes még megfigyelni, hogy a jövedelem (LG10JOV) együtthatója negatívra változott: ez azt jelenti, hogy a legnagyobb tét esetében a jövedelem nagyságával, a többi tényezõ változatlansága mellett, negatívan függ össze a kockázatvállalási hajlandóság.
A regressziós eljárást lefuttattuk úgy is, hogy kiindulva a teljes modellbõl, a nem szignifikáns változókat fokozatosan kivontuk (backstep eljárás). Ezzel eljuthattunk "tiszta" regressziós egyenletekhez. Ezekben már csak olyan együtthatók szerepelnek, amelyek csak a tényleges magyarázó változók modellben történõ figyelembe vételekor alakultak ki. Ezeket az együtthatókat a 10. táblázat foglalja össze.
A 10. táblázatban bemutatott együtthatók segítségével most már felírhatjuk, hogy hogyan is alakul a kockázatvállalás valószínûsége a modellben szereplõ magyarázó változók függvényében. Vegyük példának egy olyan válaszadót, akinek a családjában 40 000 forint az egy fõre jutó jövedelem, õ maga 29 év alatti (KOR = 1), felsõfokú végzettségû (ISKOLA3 = 3), férfi (NEM = 1). Az õ esetében annak valószínûségét, hogy az elsõ fordulóban a játékot fogja választani, a következõképpen számíthatjuk ki.
10. táblázat
A három regressziós modell eredményei: az egyes
magyarázóváltozók együtthatói
a "tiszta"regressziós egyenletekben
|
Megnevezés
|
|
|
(JÁTÉK 1 ) |
(JÁTÉK 2 ) |
(JÁTÉK 3 ) |
|
| Szabadságfok |
|
|
|
| Szignifikanciaszint |
|
|
|
| Modell ?2 |
|
|
|
| Helytállóelõrejelzések aránya |
|
|
|
| Változó |
|
| Konstans |
|
|
|
| Lg10JOV |
|
|
|
| KOR |
|
|
|
| ISKOLA 3 |
|
|
|
| NEM |
|
|
|
| ONALLO |
|
|
|
| JATEK 1 |
|
|
|
| JATEK 2 |
|
Tudjuk, hogy lg10 (40 000)=4,61, tehát
Z = -4,5669+0,8762x4,61-0,2391x1+0,2398x3+0,1600x1=0,1127,
vagyis annak valószínûsége, hogy a fenti jellemzõkkel leírható férfi az elsõ körben a játékot fogja választani, 53 százalék. Ha azonban olyan valakit veszünk példának, akinek a családjában mindössze 15 000 forint az egy fõre jutó jövedelem, õ maga 70 év fölötti (KOR = 6), alapfokú végzettséggel rendelkezik (ISKOLA3 = 1), nõ (NEM = 0), akkor annak valószínûségét, hogy az elsõ fordulóban a játékot fogja választani, a következõképpen számíthatjuk ki:
Tudjuk, hogy lg10 (15 000) = 4,18, tehát
Z = -4,5669+0,8762x4,18-0,2391x6+0,2398x1+0,1600x0 = -2,099,
vagyis annak valószínûsége, hogy a fenti jellemzõkkel leírható nõ az elsõ körben a játékot fogja választani, 11 százalék.
A kapott eredmények könnyebb, teljesebb körû és átláthatóbb interpretációja érdekében a következõ eljárást alkalmazzuk. A szignifikáns magyarázó változóink bizonyos értékkombinációinak beállításával néhány sajátságos társadalmi típusra vonatkozóan megkíséreljük meghatározni a kockázatvállalás valószínûségét a jövedelem függvényében. Arra teszünk tehát kísérletet, hogy egyes tipikus emberekre meghatározzuk, egyéb tényezõk változatlansága mellett, a szerencsejáték-választás valószínûségének alakulását a jövedelmi helyzet függvényében.
Ezek a típusok a következõk lesznek a JÁTÉK1 modell (1000 forint várható érték) esetén:
1. 29 év alatti, felsõfokú végzettségû férfi (-29, ff, f),
2. 40-59 éves, középfokú végzettségû nõ (41-59, kf, n),
3. 70 év fölötti, alapfokú végzettségû nõ (70-, af, n).
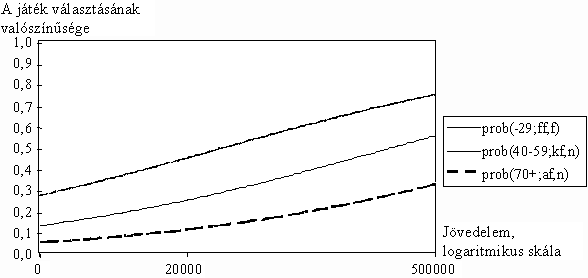
Az alábbiakban ezeknek a tipikus eseteknek a jövedelem-szerencsejáték (kockázatvállalás) függvényét rajzoljuk meg, külön-külön a három modellben. Vegyük elõször a JÁTÉK1 modellt! A 6. ábrából jól látható, hogy a kockázatvállalás valószínûsége mindegyik típus esetében emelkedik a jövedelemmel. Példánkban a legnagyobb kockázatvállalási hajlandósága a 29 év alatti felsõfokú végzettségû férfinek van, míg a szerencsejáték választásának valószínûsége a 70 év fölötti alapfokú végzettségû nõ esetében a legalacsonyabb. Érdemes megfigyelni, hogy a felsõbb jövedelemtartományokban az utóbbi típusba tartozók kockázatvállalási hajlandósága valamivel meredekebben emelkedik a jövedelem növekedésével, mint az elõbbi típusba tartozóé.
6. ábra
Az 1000 forint várható értékû
szerencsejáték választásának valószínûsége
a jövedelem függvényében, a társadalmi-demográfiai
tényezõk néhány tipikus kombinációja
esetén
A JÁTÉK2 modell (100 000 forint várható érték) esetén a következõ típusokat definiáltuk:
1. 29 év alatti, felsõfokú végzettségû férfi, akinek önálló foglalkozása van, és JÁTÉK1-ben is részt vett (-29, ff, f, o, j),
2. 40-49 éves, középfokú végzettségû nõ, aki alkalmazott, és JÁTÉK1-ben is részt vett (40-49, kf, n, a, j),
3. 40-49 éves, középfokú végzettségû férfi, aki alkalmazott, és JÁTÉK1-ben is részt vett(40-49, kf, f, a, j),
4. 70 év fölötti, alapfokú végzettségû nõ, aki alkalmazott, és JÁTÉK1-ben is részt vett(70-, af, n, a, j),
A jövedelem-JÁTÉK2 függvényt a 7. ábrán mutatjuk meg.
7. ábra
A 100 000 forint várható értékû
szerencsejáték választásának valószínûsége
a jövedelem függvényében, a társadalmi-demográfiai
tényezõk néhány tipikus kombinációja
esetén
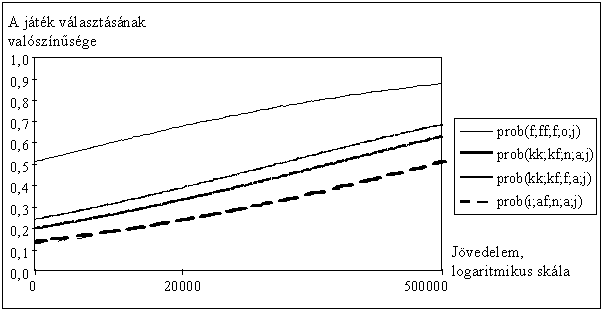
Most a felrajzolt típusaink között a kockázatvállalási valószínûségek szórása nagyobb, mint a JÁTÉK1 modell esetében volt. Ez nem meglepõ, ugyanis a középsõ játék esetében modellünk egyes változói nagyobb magyarázó erõvel rendelkeztek, mint az elõzõ példában. Megint csak azt találjuk, hogy az alacsonyabb jövedelemtartományokban a kis kockáztatási hajlandóságú típusok szerencsejáték-választási valószínûsége a magasabb jövedelemtartományokban ebben az esetben is meredekebben emelkedik, mint azoké, akik eleve szívesebben kockáztatnak.
Végezetül a JÁTÉK3 modell (1 000 000 forint várható érték) esetén a következõ tipikus eseteket definiáltuk:
1. sem a JÁTÉK1-ben, sem a JÁTÉK2-ben nem vett rész,
2. mind JÁTÉK1-ben, mind JÁTÉK2-ben részt vett.
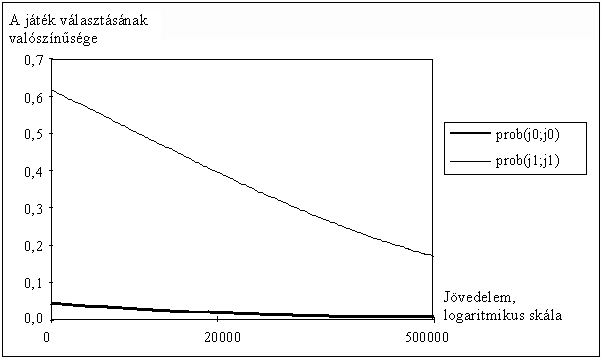
A 8. ábra mutatja be a JÁTÉK3 modellhez tartozó függvényeket. A görbék esése azt a már ismert tényt mutatja, hogy a harmadik játékra vonatkozóan a jövedelemváltozó együtthatója negatív lett. Jól látszik az a 4. táblázatban már bemutatott eredmény is, hogy a harmadik játékra már inkább csak azok maradnak meg, akik az elsõ kettõben is a játékot választották. Ez azt jelenti, hogy egy nagy tét esetén (márpedig a mai Magyarországon egymillió forint kifejezetten nagy tétnek számít) már csak azok kockáztatnak nagy valószínûséggel, akik viszonylag alacsonyabb jövedelemmel rendelkeznek, és egyébként is szeretnek játszani (részt vettek mindkét korábbi játékban).
8. ábra
Az 1 000 000 forint várható értékû
játék választásának valószínûsége
a jövedelem függvényében, az alacsonyabb várható
értékû játékokban való részvétel,
illetve az azoktól való tartózkodás esetén
A modell illeszkedése: néhány finomítás
Modellünk illeszkedésének vizsgálatára, magyarázó erejének javítására két lépcsõben teszünk kísérletet. Elõször megvizsgáljuk milyen következménye lehet annak, ha tekintettel vagyunk arra, hogy a jövedelmek és a szerencsejáték választásának valószínûsége között nem találtunk teljesen lineáris összefüggéseket. Másodsorban azt vizsgáljuk, mi történik, ha lazítjuk a modell illeszkedésének alapértelmezésként használatos kritériumait.
A nem lineáris kapcsolatok vizsgálata. A tanulmány korábbi részében, a H3. hipotézissel kapcsolatban megállapítottuk, hogy a megkérdezettek jövedelme és a játék választásának valószínûsége közti összefüggés sajátos J alakot mutat. Mivel a logisztikus regressziós elemzés feltételezései közé tartozik az is, hogy a függõ és a független változó között lineáris legyen a kapcsolat, valamiképpen kezelnünk kell ezt a problémát. A 3., 4. és 5. ábra tüzetesebb vizsgálata során intuitív módon is megállapíthatjuk, hogy a J mélypontja valahol a jövedelmek mediánjának fele körül van. Ettõl lefelé és felfelé egyaránt többé-kevésbé lineárisnak tûnõ összefüggést láthatunk. Megvizsgálhatjuk ezért azt, hogy a szóban forgó jövedelemnagyságnál többel, illetve kevesebbel rendelkezõk között külön-külön milyen eredményeket kapunk a kockázatvállalási hajlandóság magyarázatára.
Ezeknek az adatoknak az összefoglalását mutatja a 11. táblázat. Látható, hogy a szegények és a nem szegények különválasztása némiképpen változtat a kapott eredményeken. A legalacsonyabb tét esetében a jövedelem és az életkor csak a nem szegények között gyakorol szignifikáns hatást a játék választásának valószínûségére. A szegények között viszont a jövedelem és a kor hatása nem szignifikáns, az iskolának és a nemi hovatartozásnak viszont erõsebb a hatása. A foglalkozás önálló státusának egyik csoportban sincs jelentõsége. A legmagasabb tét esetében továbbra is alig találunk szignifikáns magyarázó változót. A szegények között csak az tesz különbséget ebbõl a szempontból, hogy önálló foglalkozású vagy alkalmazott-e az illetõ. A nem szegények között a jövedelem növekedésével csökken a kockáztatási hajlandóság.
11. táblázat
A három regressziós modell eredményei: az egyes
magyarázó változók együtthatói
az egész népességre együtt, valamint a
szegénységi küszöb alatti és feletti népességre
külön-külön lefutatott backstep eljárások
után, a játék egyes szintjein
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
| Szabadságfok |
4
|
3
|
2
|
6
|
4
|
2
|
2
|
2
|
2
|
| Szignifikancia |
0,0000
|
0,0000
|
0,0191
|
0,0000
|
0,0000
|
0,0000
|
0,0000
|
0,0000
|
0,0000
|
| Modell ?2 |
144,672
|
132,907
|
7,918
|
693,180
|
612,225
|
60,897
|
362,276
|
332,410
|
30,935
|
| Helytálló elõrejelzések aránya |
68,59
|
67,8
|
78,63
|
85,95
|
84,89
|
91,06
|
93,2
|
93,05
|
95,08
|
| Konstans |
-4,5669
|
-6,4153
|
-2,2366
|
-7,7045
|
-9,6719
|
-6,3241
|
-0,1523
|
0,0487
|
-4,0099
|
| B | |||||||||
| lg10JOV |
0,8762
|
1,3101
|
n. sz.
|
0,8088
|
1,3558
|
n. sz.
|
-0,869
|
-0,9255
|
n. sz.
|
| KOR |
-0,2391
|
-0,2555
|
n. sz.
|
-0,0936
|
-0,0881
|
n. sz.
|
n. sz.
|
n. sz.
|
n. sz.
|
| ISKOLA3 |
0,2398
|
0,1985
|
0,4734
|
0,2378
|
n. sz.
|
1,1218
|
n. sz.
|
n. sz.
|
n. sz.
|
| NEM |
0,16
|
n. sz.
|
0,7203
|
0,2491
|
n. sz.
|
n. sz.
|
n. sz.
|
n. sz.
|
n. sz.
|
| ONALLO |
n. sz.
|
n. sz.
|
n. sz.
|
0,7679
|
0,8102
|
n. sz.
|
n. sz.
|
n. sz.
|
2,5347
|
| JATEK1 |
|
|
|
3,3653
|
3,327
|
3,995
|
n. sz.
|
n. sz.
|
n. sz.
|
| JATEK2 |
|
|
|
|
|
|
3,5797
|
3,6618
|
3,4972
|
Ismét megfigyelhetjük, hogy a magyar jövedelemeloszlás sajátosságait is figyelembe véve, valószínûleg a százezer forintos tét az a releváns összeg, amelynek a kockáztatásával kapcsolatos magatartás a legtöbb dimenzióban vizsgálható. Ugyanakkor a szegények között még itt is mindössze az elõzõ játékban való részvétel és az iskolai végzettség differenciál. A nem szegények között viszont nincs szerepe sem az iskolának, sem a nemi hovatartozásnak: magyarázó hatása van viszont a jövedelemnek, az életkornak, az önálló foglalkozásnak és a játék elsõ fordulójában való részvételnek.
A 9., 10. és 11. ábrák - hasonlóképpen a kockáztatási valószínûségfüggvények korábbi, a 6., 7. és 8. ábrákban mutatott prezentációihoz - egy-egy tipikus személy esetében mutatják a kockázatvállalási valószínûséget a jövedelem függvényében, a szegényekre és a nem szegényekre külön-külön futtatott regressziós elemzések eredményei alapján.
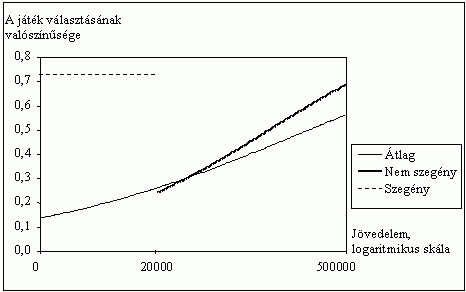
A 9. ábra azt mutatja, hogy a medián jövedelmek fele alatti sávban egy 40-49 éves, középfokú végzettségû, szegény nõ elég nagy, több mint hetvenszázalékos valószínûséggel fogja az ajándékba kapott ezer forintot kockáztatni, függetlenül attól, hogy mekkora a jövedelme ezen belül. A nem szegények között azonban mintegy 140 ezer forint között lehet az a határ, ahol az illetõ 50 százaléknál nagyobb valószínûséggel fog kockáztatni. Megfigyelhetjük még azt is, hogy ha a nem szegényeket és a szegényeket külön vizsgáljuk, akkor a nem szegények között a jövedelem magyarázó ereje nagyobb lesz.
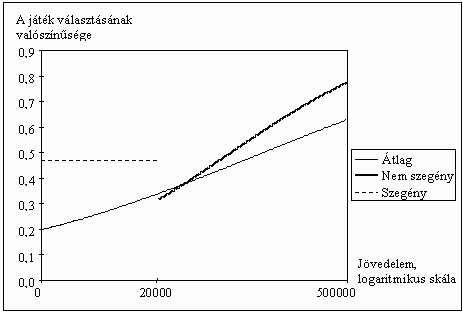
A 10. ábra ugyanerre a személyre a százezer forintos tét esetében mutatja a kockázatvállalási valószínûséget. Az átlaghoz képest vett elmozdulás iránya most is nagyon hasonló ahhoz, amit az elõbbiekben láttunk, két megszorítással. Elõször is, a szegények között a kockáztatási hajlandóság, noha itt sem függ a jövedelemtõl, alatta marad az 50 százaléknak. Másodsorban viszont a nem szegények között alacsonyabb (mintegy 80 ezer forint háztartásjövedelem körüli) az a jövedelemhatár, amikor a kockáztatás valószínûsége az 50 százalékot meg fogja haladni.
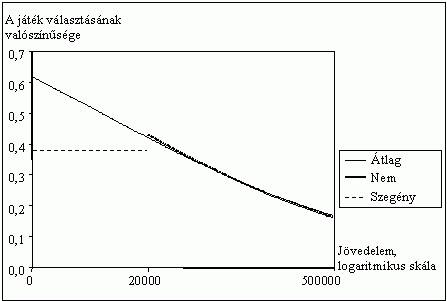
A 11. ábrán, mivel a vizsgált társadalmi-demográfiai változók nem voltak szignifikánsak, tipikus személyünket az elsõ két játékban való részvétellel definiáltuk. Láthatjuk, hogy még az õ esetükben is minden jövedelmi sávban 50 százalék alatt marad a kockáztatás valószínûsége, továbbá ez a valószínûség a nem szegények között a jövedelem növekedésével erõsen csökken.
9. ábra
Az 1000 forint várható értékû
játék választásának valószínûsége
a jövedelem függvényében: középfokú
végzettségû, 40-49 éves nõ, a medián
50 százaléka alatti és fölötti jövedelmekre
külön futtatott regressziós modellek alapján
10. ábra
A 100 000 forint várható értékû
játék választásának valószínûsége
a jövedelem függvényében: középfokú
végzettségû, 40-49 éves nõ, aki az elsõ
játékban is játszott, a medián 50 százaléka
alatti és fölötti jövedelmekre külön futtatott
regressziós modellek alapján
A modellilleszkedés valószínûségi kritériumainak enyhítése. Több módszer is rendelkezésre áll annak eldöntésére, hogy logisztikus regressziós modelljeink mennyire jól illeszkednek az adatokhoz. A korábbiakban elemzett modelljeink egyik illeszkedési kritériumaként a modell által helytállóan elõre jelzett esetek arányát használtuk. A 11. táblázatunkban például láthattuk, hogy a százezer forintos tét esetén a helytállóan elõre jelzett esetek aránya a nem szegény népességben 84,9 százalék volt, modellünk illeszkedését tehát ez alapján viszonylag jónak mondhatjuk.
Idõzzünk most el egy kicsit annál, mit is jelent mindez! A 12. táblázat részletesen mutatja a szóban forgó modellre vonatkozó klasszifikációs táblát. Ebbõl látható, hogy 1601 esetre azért volt helytálló az elõrejelzés, mert modellünk ennyi emberre jelzett elõre passzivitást a játék második fordulójában, s õk valóban nem is játszottak. Összesen 112 olyan esetünk volt, akiket játékosnak jeleztünk, és õk valóban játszottak is. Ez az összesen 1713 eset az összes nem szegény népességnek (2018 fõnek) pontosan 84,9 százaléka volt.
11. ábra
Az 1 000 000 forint várható értékû
játék választásának valószínûsége
a jövedelem függvényében, s a megkérdezett
az elsõ két játékban is részt vett,
a medián 50 százaléka alatti és fölötti
jövedelmekre külön futtatott regressziós modellek
alapján
12. táblázat
Klasszifikációs táblázat: nem szegények,
100 000 forint tét esetén, p>0,5 valószínûség
mellett
|
|
|
||||
|
|
|
|
|
||
| Nem játszik | N |
1601
|
230
|
1831
|
|
| az összes százalékában |
79,3
|
11,4
|
90,7
|
||
| Játszik | N |
75
|
112
|
187
|
|
| az összes százalékában |
3,7
|
5,6
|
9,3
|
||
| Összesen | N |
1676
|
342
|
2018
|
|
| százalék |
83,1
|
16,9
|
100
|
||
| Helytálló elõrejelzések aránya: |
|
||||
Az efféle klasszifikációs táblázatokban az elõrejelzés "jóságának" kritériuma az, hogy a szóban forgó esetre nézve a játék választásának valószínûsége 50 százalék alatt van, vagy esetleg meghaladja azt. Ha 50 százalék alatt van, akkor a modell szerint az illetõ nem fogja a játékot választani. Ha az adott valószínûségi érték 50 százalék fölött van, akkor viszont játszani fog. Vizsgáljuk most meg, hogy az adott esetben miképpen fest a játék elõre jelzett választásának valószínûségének eloszlása az adott nem szegény népességben! Ezt mutatja a 13. táblázat utolsó sora. Modellünk alapján az összes 2018 személy 66,8 százalékára (1349 fõre) mondhatjuk azt, hogy az õ esetükben 10 százalék alatt van a játék választásának valószínûsége. Összhangban eddigi eredményeinkkel, némiképpen több mint 9 százalék lenne a több mint ötvenszázalékos valószínûséggel játszók aránya. Van azonban összesen 464 olyan emberünk, akikre legalább harmincszázalékos valószínûséggel mondhatjuk, hogy elõrejelzésünk szerint részt venne a játékban.
Természetesen nem minden olyan megkérdezettünk fog ténylegesen a játék mellett dönteni, akire ezt mi elõre jeleztük. Az elõre jelzett játszási valószínûséggel együtt növekszik azonban annak esélye, hogy az illetõ ténylegesen is játszani fog. Ezt a 13. táblázatban a játszik (alulról a 3. és a 4.) sor mutatja. Például láthatjuk, hogy 135 olyan esetünk van, amelyre a modell 40 és 50 százalék közöttire teszi annak valószínûségét, hogy õk a játék mellett fognak dönteni. Láthatjuk, hogy közöttük 43 százalék azok aránya, akik ténylegesen a játékot választották.
Az ötvenszázalékos elfogadási kritérium enyhítésével megvizsgálhatjuk, hogy magasabb lesz-e a modell helytálló elõrejelzéseinek aránya. Egy ilyen klasszifikációs táblát mutat be a 14. táblázat. Ezt összevetve a 12. táblázattal, megállapíthatjuk, hogy az elfogadási kritérium lazításával jelentõsen megnõne a modell által "játékosként" elõre jelzett esetek aránya (9,3 százalékról 32,3 százalékra). A ténylegesen a játékot választók aránya azonban e két érték között, 17 százalék körül mozgott. Az elfogadási kritérium lazítása tehát esetünkben azzal is együtt járna, hogy nagymértékben megnõne azoknak az aránya is, akiket úgy prognosztizáltunk játékosnak, hogy valójában passzívak maradtak. Összességében tehát az elfogadási kritérium ilyen lazítása nem javítaná, hanem rontaná a helytálló elõrejelzések arányát (84,9 százalékról 80,6 százalékra).
13. táblázat
Részletes klasszifikációs táblázat,
nem szegények, 100 000 forint tét esetén
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||
| Nem játszik | N |
1312
|
14
|
98
|
177
|
61
|
13
|
1
|
1676
|
|
| Oszlop-
százalék |
97,3
|
77,8
|
64,5
|
56,7
|
43,6
|
39,4
|
7,1
|
83,1
|
||
| Játszik | N |
37
|
4
|
54
|
135
|
79
|
20
|
13
|
342
|
|
| Oszlop-
százalék |
2,7
|
22,2
|
35,5
|
43,3
|
56,4
|
60,6
|
92,9
|
16,9
|
||
| Összesen | N |
1349
|
18
|
152
|
312
|
140
|
33
|
14
|
2018
|
|
| Sors-
zázalék |
66,8
|
0,9
|
7,5
|
15,5
|
6,9
|
1,6
|
0,7
|
100
|
||
14. táblázat
Összevont klasszifikációs tábla, nem szegények,
100 000 forint tét esetén, p>0,3 valószínûség
mellett
|
|
|
||||
|
|
|
|
|
||
| Nem játszik | N |
1326
|
41
|
1367
|
|
| az összes százalékában |
65,7
|
2,0
|
67,7
|
||
| Játszik | N |
350
|
301
|
651
|
|
| az összes százalékában |
17,3
|
14,9
|
32,3
|
||
| Összesen | N |
1676
|
342
|
2018
|
|
| százalék |
83,1
|
16,9
|
100
|
||
| Helytálló elõrejelzések aránya |
80,6
|
||||
Ugyanezt az eljárást lefolytattuk a szegények esetében
is, hasonló eredménnyel. Az elfogadási kritérium
lazítása a játékosnak elõre jelzettek
arányát 5,8 százalékról 12,9 százalékra
emelte volna, ezzel azonban a helytálló elõrejelzések
aránya 92,4 százalékról 91 százalékra
esett volna (F7. és F8. táblázat).
Összefoglalás
Tanulmányunkban a kockázattal szembeni attitûd empirikus elemzésére tettünk kísérletet. Gondolatmenetünk kiindulópontjaként elfogadtuk a racionális döntések elméletének alapfogalmait és analitikus modelljeit. A bizonyosság, bizonytalanság és kockázat megkülönböztetése után definiáltuk a kockázattal szembeni attitûd három alaptípusát: a kockázatkerülést, a kockázatsemlegességet és a kockázatkedvelést. Gondolatmenetünk irányát ezután azonban már nem a racionális döntések elméletének normatív kérdésfelvetései szabták meg: Nem arra voltunk kíváncsiak, hogy mekkora az optimális kockázatvállalási hajlandóság vagy mekkora mértékû kockázatot kell a tökéletesen racionális döntéshozónak vállalnia.17 Inkább az érdekelt bennünket, hogy a rendelkezésünkre álló - viszonylag kevés - empirikus adat alapján milyen összefüggéseket tudunk feltárni a kockázattal szembeni attitûd empirikus típusairól, azok társadalmi-demográfiai meghatározottságáról. A racionális döntések elméletét tehát mindenekelõtt fogalomtisztázási és hipotézisalkotási célokra használtuk: Az empirikus ellenõrzésre váró hipotézisek egy részét - a tipikus kockázattal szembeni attitûdre, valamint a kockázattal szembeni attitûd és a tét nagysága, illetve a jövedelem nagysága közti összefüggésekre vonatkozó hipotéziseket - az elméleti modellekbõl származtattuk. A többi hipotézist - a kockázattal szembeni attitûd társadalmi-demográfiai összefüggéseirõl - részben korábbi empirikus eredményekre támaszkodva, részben intuitíve fogalmaztuk meg.
Empirikus elemzésünket az egyes részhipotézisek - viszonylag egyszerû (például kereszttáblás) - ellenõrzésével kezdtük. Adataink alátámasztották alaphipotézisünket, miszerint a kockázattal szembeni attitûd tipikus formája a kockázatkerülés, ugyanakkor rávilágítottak arra a tényre is, hogy - még viszonylag nagy tét esetén is - elõfordul a kockázatkedvelés. A tétek nagysága és a kockázatkerülés közti kapcsolatra vonatkozó hipotézisünket szintén megerõsítették adataink: A tétek emelkedésével egyértelmûen csökken a kockázatvállalási hajlandóság. Ugyanakkor a jövedelemnagyság és a kockázatkerülés közti kapcsolatra vonatkozó kezdeti hipotézisünket az empirikus eredmények alapján több szempontból is finomítani kellett: Egyrészt világossá vált, hogy a tét és a jövedelem együtt ragadja meg azokat az összefüggéseket, amelyeket a döntéshozók relatív jövedelmi helyzetében bekövetkezett változásokként értelmeztünk korábban, s ezért az elemzés során hatásukkal együtt kell számolni. Másrészt adataink szerint a kockázatvállalási hajlandóság a jövedelmek emelkedésével nem lineárisan, hanem inkább sajátos J mintát követve alakul: a kicsi relatív jövedelemváltozást eredményezõ döntési helyzetekben inkább számíthatunk valamivel nagyobb arányú kockázatkedvelésre, mint a nagy relatív jövedelemváltozást eredményezõ döntési helyzetekben. A kockázattal szembeni attitûd társadalmi-demográfiai tényezõi közül az iskolai végzettség hatását csak részben, a foglalkozás hatását differenciáltan, míg az életkor és a nemi hovatartozás hatását elsõ közelítésben elég egyértelmûen látszottak megerõsíteni adataink. Ezeket az eredményeket mindazonáltal csak fenntartásokkal fogadhattuk el a lehetséges összetételi hatások miatt. Ezért a további elemzés során szükségesnek tartottuk elvégezni az adatok többváltozós statisztikai elemzését, logisztikus regressziós modellek segítségével.
A többváltozós elemzés szerint a legkisebb tét esetén a jövedelem és az iskolai végzettség gyakorol szignifikáns (pozitív) hatást a kockázatvállalási hajlandóságra, míg a közepes tét esetén valamennyi változó hatása szignifikáns: erõsebben hat a jövedelem, az életkor, az önálló foglalkozási státus, valamint az, ha a vizsgált személy az alacsonyabb tét esetében kockáztatott, gyengébben az iskolai végzettség és a nemi hovatartozás. A legmagasabb tét esetén csupán két szignifikáns magyarázó változónk maradt: a jövedelem és az, ha az érintett a közepes tét esetén kockáztatott (ráadásul a jövedelem hatása megfordult). Az elemzés plasztikusabbá tétele céljából végül különbözõ tipikus - s általunk érdekesnek ítélt - döntéshozókat definiáltunk, s több szempontból finomítottuk a modell illeszkedését. Ennek során mindenekelõtt azt vizsgáltuk, hogyan változik ezeknek a hipotetikus döntéshozóknak a kockázatvállalási hajlandósága a jövedelem függvényében. Eredményeink azt mutatják, hogy a kicsi és a közepes tét esetében a kockázatvállalási hajlandóság nõ a jövedelem emelkedésével, míg a legmagasabb tét esetén megfordult az összefüggés. Többváltozós elemzéseink finomításainak egyik további tanulsága, hogy a magyar jövedelmi viszonyok között leginkább a közepes nagyságú tét (100 000 forint) esetén kapott eredményeket tekinthetjük leginkább elfogadhatónak.
Végül utalunk arra, hogy alapvetõen kétféle
további elemzési irányt tartunk követendõnek
az általunk tárgyalt kérdéskörben. Egyrészt,
követve a kockázatvállalási hajlandósággal
foglalkozó empirikus vizsgálódások fõirányát,
finomabban megfogalmazott kísérleti kérdésekkel
kívánjuk mérni a kockázatkerülés
mértékét a jövõben. Nemcsak arra vagyunk
kíváncsiak, hogy hogyan oszlik meg a népesség
az alapvetõ kockázatpreferenciák alapján, hanem
finomabb mércével kívánjuk a kockázatkerülés
mértékét közelíteni. Másrészt
a jövõben tervezzük nem kísérleti, hanem
természetes döntések (például biztosításkötések,
befektetések) hasonló szempontú empirikus elemzését,
s ezen eredmények összevetését a kísérleti
vizsgálatok adataival. Az effajta adatok jól kiegészíthetik,
s adott esetben korrigálhatják a steril kísérleti
adatokat.
Hivatkozások
Becker, G. S. 1998. Értékek és preferenciák. In: Lengyel György-Szántó Zoltán (szerk.): Tõkefajták: Társadalmi és kulturális erõforrások szociológiája. Budapest: Aula
Becker, G. S.-G. J. Stigler. 1989. De Gustibus Non Est Disputandum. In: G. J. Stigler (ed.) Piac és állami szabályozás. Budapest: Közgazdasági és Jogi Könyvkiadó
Csontos László 1995. Fiskális illúziók, döntéselmélet és az államháztartási rendszer reformja. Közgazdasági Szemle, 2.
- 1998. A racionális döntések elmélete. Budapest: Osiris
Csontos László-Tóth István György 1998. Fiskális csapdák és államháztartási reform az átmeneti gazdaságban. In: Gács János-Köllõ János (szerk.): A túlzott központosítástól az átmenet stratégiájáig. Tanulmányok Kornai Jánosnak. Budapest: Közgazdasági és Jogi Könyvkiadó
Csontos László-Kornai János-Tóth István György 1996. Adótudatosság és fiskális illúziók. In: Andorka Rudolf-Kolosi Tamás-Vukovich György: Társadalmi Riport 1996. TÁRKI. Budapest
Elster, J. 1986. Introduction. In: J. Elster (ed.) Rational Choice. New York: New York University Press
- 1995. A társadalom fogaskerekei. Magyarázó mechanizmusok a társadalomtudományban. Budapest: Osiris
Hirsleifer, J.-J. G. Riley 1992. The Analytics of Uncertainty and Information. Cambridge: Cambridge University Press
- - 1998. A bizonytalanságban hozott döntések elemei. In : Csontos (szerk.) 1998.
Kagel, J. H.-A. R. Roth (eds.) 1995. The Handbook of Experimental Economics. Princeton: Princeton University Press
Kahneman, D.-A. Tversky 1991. A döntések megfogalmazása és a választás pszichológiája. In: Nagy Péter-Pápai Zoltán (szerk.) Döntéselmélet. Szöveggyûjtemény. Budapest: Aula
- - 1998. Kilátáselmélet: a kockázatos helyzetekben hozott döntések elemzése. In: Csontos 1998.
Morrow, J. D. 1994. Game Theory for Political Scientists. Princeton: Princeton University Press
Thaler, R. H. 1987. The Psychology of Choice and the Assumptions of Economics. In: A. Roth (ed.) Laboratory Experiments in Economics: Six Points of View. New York: Cambridge University Press
Thaler, R. H.-E. J. Johnson 1990. Gambling with the House Money and Trying to Break Even: The Effects of Prior Outcomes on Risky Choices. Management Science, 6.
Varian, H. 1991. Mikroökonómia középfokon.
Budapest: Közgazdasági és Jogi Könyvkiadó
Függelék
F1. táblázat
A szerencsejátékot választók aránya
a különbözõ jövedelemszinteken, különbözõ
jövedelemfogalmak esetén
|
százalékában (csak pozitív jövedelmek) |
jövedelem |
jövedelem |
jövedelem |
|
|
|
||
| -50 |
|
|
|
| 51-80 |
|
|
|
| 81-120 |
|
|
|
| 121-160 |
|
|
|
| 161- |
|
|
|
|
|
|
||
| -50 |
|
|
|
| 51-80 |
|
|
|
| 81-120 |
|
|
|
| 121-160 |
|
|
|
| 161- |
|
|
|
|
|
|
||
| -50 |
|
|
|
| 51-80 |
|
|
|
| 81-120 |
|
|
|
| 121-160 |
|
|
|
| 161- |
|
|
|
F2. táblázat
Az elsõ fordulóban (1000 forint) válaszadók
megoszlása a háztartás összes jövedelmek,
az egy fõre jutó jövedelmek és a személyes
jövedelmek kategóriáiban
|
százalékában (csak pozitív jövedelmek) |
jövedelem |
jövedelem |
jövedelem |
| -50 |
|
|
|
| 51-80 |
|
|
|
| 81-120 |
|
|
|
| 121-160 |
|
|
|
| 161 |
|
|
|
| Összesen |
|
|
|
| N |
|
|
|
F3. táblázat
A kockázatvállalók (szerencsejátékot
választók) aránya az egyes iskolai végzettségi
csoportokban, a tétek különbözõ szintjein
| Iskolai |
|
|
||
| végzettség |
|
|
|
|
| 8 általános alatt |
|
|
|
|
| 8 általános |
|
|
|
|
| Szakmunkásképzõ |
|
|
|
|
| Szakközépiskola |
|
|
|
|
| Gimnázium |
|
|
|
|
| Fõiskola |
|
|
|
|
| Egyetem |
|
|
|
|
F4. táblázat
A kockázatvállalók (szerencsejátékot
választók) aránya az egyes életkori csoportokban,
a tétek különbözõ szintjein
| Életkor |
|
|
||
|
|
|
|
|
|
| -29 |
|
|
|
|
| 30-39 |
|
|
|
|
| 40-49 |
|
|
|
|
| 50-59 |
|
|
|
|
| 60-69 |
|
|
|
|
| 70- |
|
|
|
|
F5. táblázat
A játékot választók aránya különbözõ
tétek mellett, korcsoport és iskolai végzettség
szerint, százalék
| Év |
|
||
|
|
|
|
|
|
|
|||
| -39 |
|
|
|
| 40-59 |
|
|
|
| 60- |
|
|
|
|
|
|||
| -39 |
|
|
|
| 40-59 |
|
|
|
| 60- |
|
|
|
|
|
|||
| -39 |
|
|
|
| 40-59 |
|
|
|
| 60- |
|
|
|
F6. táblázat
A kockázatvállalók (szerencsejátékot
választók) aránya a különbözõ
foglalkozási csoportokban, a tétek különbözõ
szintjein
| Megnevezés |
|
|
||
|
|
|
|
||
| Utolsó foglalkozás | ||||
| Sosem dolgozott |
|
|
|
|
| Mezõgazdasági fizikai
foglalkozású |
|
|
|
|
| Önálló |
|
|
|
|
| Szakképzetlen munkás |
|
|
|
|
| Szakmunkás |
|
|
|
|
| Alsó vezetõ |
|
|
|
|
| Fehérgalléros |
|
|
|
|
| Vezetõ |
|
|
|
|
| Értelmiségi |
|
|
|
|
| ?2 |
|
|
|
|
| Szabadságfok |
|
|
|
|
| Szignifikanciaszint |
|
|
|
|
| Önálló foglalkozású (volt)? | ||||
| Nem önálló |
|
|
|
|
| Önálló |
|
|
|
|
| ?2 |
|
|
|
|
| Szabadságfok |
|
|
|
|
| Szignifikanciaszint |
|
|
|
|
F7. táblázat
Klasszifikációs táblázat, szegények,
100 000 forint tét esetén, p > 0,5 valószínûség
mellett
|
|
|
||||
|
|
|
|
|
|
|
| Nem játszik | N |
248
|
14
|
262
|
|
|
|
százalék |
89,2
|
5
|
|
94,2
|
| Játszik | N |
7
|
9
|
16
|
|
|
|
százalék |
2,5
|
3,2
|
|
5,8
|
| Összesen | N |
255
|
23
|
278
|
|
|
|
százalék |
91,7
|
8,3
|
|
100
|
| Helytálló elõrejelzések aránya |
92,4
|
|
|
||
F8. táblázat
Összevont klasszifikációs táblázat,
szegények, 100 000 forint tét esetén, p > 0,3 valószínûség
mellett
|
|
|
||||
|
|
|
|
|
|
|
| Nem játszik | N |
236
|
6
|
242
|
|
|
|
teljes százalék |
84,9
|
2,2
|
|
87,1
|
| Játszik | N |
19
|
17
|
36
|
|
|
|
teljes százalék |
6,8
|
6,1
|
|
12,9
|
| Összesen | N |
255
|
23
|
278
|
|
|
|
százalék |
91,7
|
8,3
|
|
100
|
| Helytálló elõrejelzések aránya |
91,0
|
|
|
||
1. Ez a szöveg a Cselekvéselmélet
és társadalomkutatás címmel Csontos László
emlékének dedikált mûhelykonferenciára
(Budapest, 1998. november 27-28.) készült tanulmány
átdolgozott változata. (A tanulmány megírását
az OTKA támogatta: F 022195.) A szerzõk mindketten el nem
múló hálával tartoznak Csontos Lászlónak,
aki egyszerre tanított szakmai alaposságra és emberséges
viselkedésre. A tanulmányban szereplõ ötlet akkor
merült fel, amikor e tanulmány egyik szerzõje Csontos
Lászlóval Az állam és polgárai címû
kutatás (Csontos-Kornai-Tóth 1996 és Csontos-Tóth
1998) folytatásaként a kockázattal szembeni attitûd
és a jóléti rendszerek reformjával kapcsolatos
attitûd közötti összefüggést tervezték
vizsgálni. Az itt elemzett kérdések Csontos László
javaslatára kerültek a kérdõívbe.
A szerzõk szívesen vesznek minden javaslatot és
kritikai megjegyzést a szoc_szanto@pegasus.bke.hu és a toth@tarki.hu
címen. Köszönet illeti Gál Róbert Ivánt
a konferencián tett értékes megjegyzéseiért.
2. A kockázatkerülést itt a csökkenõ
határhaszon következményeként értelmeztük,
habár származtatható közvetlenül a kockázattal
szembeni óvatos, konzervatív magatartásból
(Elster 1986: 29; 16. lábjegyzet).
3. Fontos hangsúlyoznunk, hogy itt a következmények
felett értelmezett preferenciaindex-függvényrõl
(vagy elemi haszonfüggvényrõl), nem pedig a cselekvési
alternatívák felett értelmezett haszonfüggvényrõl
van szó. E megkülönböztetés fontosságáról,
valamint a megkülönböztetés elmulasztásából
fakadó félreértésekrõl és terméketlen
vitákról lásd Hirshleifer-Riley 1998: 31-32; 37. Ennek
kapcsán azt is érdemes továbbá hangsúlyozni,
hogy a következmények felett értelmezett preferenciaindex-függvény
kardinális rendezést követel meg, míg a cselekvési
alternatívák felett értelmezett haszonfüggvény
megelégszik az ordinális rendezéssel. Az elemi haszonfüggvény
kardinalizálása - például a fent körvonalazott
referencialutri-eljárás révén (uo. 34-35.)
- nélkülözhetetlen technikai elõfeltétele
a várhatóhasznosság-szabály alkalmazásának.
4. Ez matematikailag kifejezve annyit jelent, hogy
mindhárom elemi haszonfüggvény elsõ deriváltja
pozitív: a függvény emelkedõ, a következmény
(például jövedelem) határhaszna pozitív.
Ez - mondjuk - azt a tartalmi összefüggést fejezi ki,
hogy a nagyobb jövedelem jobb, mint a kisebb. A függvény
második deriváltja kockázatsemlegesség esetén
nullával egyenlõ, kockázatkerülés esetén
negatív, kockázatkedvelés esetén viszont pozitív:
a függvény állandó, csökkenõ, illetve
növekvõ ütemben emelkedik. A három eset közül
a kockázatkerülés tekinthetõ "normálisnak"
abban az értelemben, hogy ez tükrözi a csökkenõ
határhaszon tendenciáját. Ezt támasztja alá
az az általános tapasztalat is, hogy az emberek portfóliója
általában diverzifikált (Hirshleifer-Riley 1998: 44).
5. Az elmélet ezen feltevésének
feloldásához és a várhatóhasznosság-szabály
konstruktív kritikájához lásd mindenekelõtt
Kahneman-Tversky (1991; 1998), immár klasszikus modelljét
(kilátáselmélet), valamint Thaler (1987) áttekintését.
A kifejtésben elsõsorban Csontos (1995), valamint Thaler-Johnson
(1990) gondolatmenetére támaszkodunk.
6. Jó áttekintés a kísérleti
közgazdaságtan döntéselméleti ágáról:
Kagel-Roth (1995). Azok közül a döntéspszichológiai
kísérletek közül, amelyek eredményeire magyarázattal
szolgál a kilátáselmélet, érdemes külön
is kiemelni azokat, amelyek a döntési probléma megfogalmazásából
fakadó hatásokat (framing effects) tesztelik. Ha gyakorlatilag
ugyanazt a döntési problémát megfogalmazzuk nyereségek
és veszteségek terminusaiban, általában szignifikánsan
eltérõ preferenciaeloszlást kapunk, ami egyértelmûen
aláhúzza a döntési probléma megfogalmazásának
jelentõségét. Vegyük illusztrációképpen
Kahneman és Tversky klasszikus kísérletei közül
a következõt. (Idézi: Thaler (1987), zárójelben
az egyes alternatívákat választó kísérleti
alanyok aránya szerepel.)
Tegyük fel, hogy Ön 300 dollárral gazdagabb, mint jelenleg. Válasszon az alábbi két lehetõség közül:
| A: Biztosan nyer 100 dollárt | (72%) |
| B: 50 százalék eséllyel nyer 200 dollárt, és 50 százalék eséllyel semmit | (28%) |
| A: Biztosan veszít 100 dollárt | (36%) |
| B: 50 százalék eséllyel veszít 200 dollárt, és 50 százalék eséllyel semmit | (64%) |